背景

1960年夏，肖斯塔科维奇以苏联杰出艺术家的身份，为反映德累斯顿大轰炸的苏联电影《五天五夜》创作配乐。他在配乐时，仅花了三天时间（7月12日-7月14日）便完成了这部弦乐四重奏。它的创作背景和意图最初被认为一目了然——作者本人在标题下写道：“献给法西斯主义战争受难者”，同时在1960年9月24日的《消息报》中刊登了对肖斯塔科维奇的采访：“我在与德累斯顿的当地居民聊天中得知，这些人都是在疯狂的轰炸中得以幸存的，从他们悲伤绝望的语气中，我感受到了那是多么可怕的经历。为电影配乐的这几天，影片里的场景和现实悲惨的情景把我包围了，这促使我产生了新的音乐灵感，在这三天的工作中，我还同时完成了一部新的弦乐四重奏的曲谱，这部作品要献给那些在战争中牺牲的人们。”——这一切似乎都证明这部弦乐四重奏仅是一部反法西斯的作品，表达了作者对战争和法西斯主义的憎恶。但是，在作曲家给好友写的信里面，他又表达了创作这部曲子更深一层的的动机：“有时我想，如果我在某时一命呜呼，未必有人能专门作曲来寄托对我的哀思。因此，我决定自己为自己先写这么一首乐曲，甚至可以在封面上写道，‘为纪念这首四重奏的作者而作’。”所以，这部弦乐四重奏同时也是一部具有自传性质的作品，表达了作曲家在那个特殊的年代压抑、恐惧、焦虑、苦闷的心情。

浅析

前排叠甲声明：本人不是音乐相关专业出身的，水平和精力有限，肯定会有知识性的不足，相关错误还请多多包涵，能友善地指出来那就更好啦！

整体结构和特色

这部弦乐四重奏由五个乐章组成，中间不间断演奏：

• 第一乐章：广板 (Largo)
• 第二乐章：很快的快板 (Allegro molto)
• 第三乐章：小快板 (Allegretto)
• 第四乐章：广板 (Largo)
• 第五乐章：广板 (Largo)

这部作品开篇就用了肖斯塔科维奇的签名动机——D(D)S(Eb，德国音乐符号中记作S)C©H(B，德国音乐符号中记作H)并贯穿所有乐章。同时，这部作品还体现了肖斯塔科维奇作品的另一个特征：“自我引用乐段”。他在这部作品里巧妙地融合了自己的《f小调第一交响曲》开头动机、《e小调第二钢琴三重奏》末乐章的一个主题、《降E大调第一大提琴协奏曲》开头主题和《姆岑斯克县的麦克白夫人》第四幕女主人著名唱段等多个乐段。

第一乐章：三部曲式

第一乐章的开头由大提琴在低音部拉出“D-Eb-C-B”三个音，随后紧接着由中提琴、第二小提琴、第一小提琴在不同声部上拉出这段旋律，形成密接合应。缓慢的速度和不和谐的音程（D-Eb和C-B都是小二度）营造出压抑的氛围。

第一乐句终止后引入了《f小调第一交响曲》开头的动机——但和第一交响曲营造的氛围完全不同，第一交响曲在小快板(Allegretto)的速度下，用巴松、小号等乐器演奏这段旋律，和附点节奏一起共同营造了神秘的氛围；而在这部弦乐四重奏里，用更慢的速度演绎相同的旋律，却营造了低沉悲伤的氛围，仿佛置身于天气阴沉葬礼上，周围有乌鸦盘旋。

DSCH动机过渡之后便是一串下行半音阶，诉说着作曲家心里的悲伤与不安。随后，大提琴在低音部再次奏响DSCH，然后一直保持着C音，同时高音部的两把小提琴保持着旋律的进行，这样便在悲伤的氛围里更增一分紧张——紧张着随时都有可能来的灭顶之灾。

低落的旋律盘旋了一会后，第一小提琴引入了新的主题，整个乐章便进入了第二部分。首先第一小提琴的旋律色彩似乎明亮了一些。他尝试着让这种光芒持久点——但下行的旋律似乎在暗示着这种努力是徒劳的。下行后又回到了第二部分开始的E音，这次的旋律在C大调上尝试上行——但插入的降E却增添了一抹浓重的悲凉色彩。第一小提琴在不断地尝试着明亮昂扬，但第二小提琴的旋律依然沿袭着之前的悲伤，同时中提琴和大提琴保持的音依然营造着紧张苦闷的氛围。最后，第一小提琴再次奏响“DSCH”（同时伴随着渐强的记号），代表着它尝试塑造的泡沫彻底破碎。挽歌式的旋律在不同声部交替出现，不停盘旋。

第一小提琴和第二小提琴再次拉响“DSCH”——于是我们进入了这篇乐章的第三部分。这一部分是第一部分主题的再现，也和第一部分一样出现了慢版的《第一交响曲》动机。最后，在第二小提琴、中提琴和大提琴合奏的长音升G中（同时这里的升G有种暴风雨前的躁动感！），我们迎来了第二乐章。

第二乐章：奏鸣曲式

稍微吐槽一下某社长：第一遍问他是不是奏鸣曲式时他说成二部曲式了……后来他自己发现问题了。现在已经改过来啦

第二乐章由升g小调开始，整个乐章的调性在升g小调、c小调等多个调性间切换。主部主题动机伴随着极快的速度和“ff”甚至“sfff”的强度，给人极度焦虑扭曲的感觉。该乐章第一部分的前半段大量采用了半音阶音级：先是第一小提琴不停地半音阶上下行，然后一个“DSCH”四个音的过度，半音阶的滚动转移到了中提琴和大提琴，第一和第二小提琴则用下弓和双音进行配合——渲染了焦躁扭曲的情绪。同时随处可见的重音记号以及“ff”“sf”记号更是加重了这种情绪。

突然，又是DSCH在不同声部上的呈现——和第一乐章的开头很像，但这次和第一乐章的缓慢与压抑截然不同，是一种焦虑和扭曲——用极快的速度，在几个声部的来回呈现后又在高音部不停地用很强的力度刮擦着你的耳膜，像是肖斯塔科维奇在那个年代里愤怒的呐喊和控诉，表达自己对强权的永不屈服。紧接着是对本乐章开头的主题动机进行再现与变奏，同时巧妙地融入“DSCH”在其中；最后高音部“DSCH”的反复，结束了这篇乐章的第一部分。

副部由c小调开始，出现了该乐章的第二个主题动机，同时该动机引用了作曲家本人的《第二钢琴三重奏》末乐章开头的主题动机。高音部分反复着这个动机，而中音部分和低音部分出现了大量三连音，伴随着“fff”的出现，整篇乐章的情绪似乎在这一刻达到了顶点！在这里，肖斯塔科维奇的内心一览无余：在强权压迫下，他焦虑、恐惧却不愿屈服。可是那种环境，他只能用自己的音乐来发泄这些情绪，多余的话他一个字都不敢说。

该动机短暂地结束了一阵子，进入展开部。中间高音区的半音阶滚动似是肖斯塔科维奇内心孤独恐惧的真实写照。又出现了“DSCH”——不过这次主要是低音区演奏这段动机，高音区伴以另一种旋律来反复渲染焦虑、恐惧、扭曲甚至充斥着血腥的暴虐氛围。

伴随着第一个主题动机的再次出现，调性又转回了升g小调：这里是再现部，更增焦虑和暴虐。后又转入c小调，“DSCH”再现，但在第二次“DSCH”出现时，力度却突然从强变弱——强度的突变渲染了更深一层的恐怖，就像你向同门吐槽导师却突然发现导师就在你身边时一样。但这种情绪还是无法抑制——渐强的符号说明了一切——“ff”的力度下再次奏响第二个主题动机，不过这次换成中音和低音部演奏这个主题动机，高音部则不停地演奏着三连音——由升C-E-G-A上行再下行所组成的三连音。最后在终止式上，这个乐章的结束和弦是A-升C-E-G——是g小调的重属和弦，并没有落回主调性c小调上，给人意犹未尽之感。

第三乐章：三部曲式的圆舞曲

乐章的开始是一个g小调的引子段落，第一小提琴又引入了“DSCH”，而第二小提琴的颤音像警哨一样响在听者的心中。随之而来的便是带着犹太风格的主题动机。犹太风格的音乐具有常常变换节奏和调式、旋律以小音程进行等特点。~~但讲真，不是什么民族歧视，我觉得那段听起来有点鬼鬼祟祟的。~~依旧是不断重复的“DSCH”——但D音都重复了一次——且跟随着跳跃的半音阶下行、第二小提琴的颤音和中提大提的三拍子圆舞曲节奏，更给人诡异、不安的感觉，似是有什么看不见的危险在边上。

这一段结束后又引入了新的主题动机：上半音级、三连音和拨弦，还是那么诡异，令人心里发毛。这个动机短暂地出现了一会便切回了原来的犹太风格主题动机，但原来的动机也只出现了一下，便由大量不和谐的音代替。随后又是“DSCH”——这个动机几乎无孔不入——引入了另一个主题动机，同时也是他《降E大调第一大提琴协奏曲》第一乐章里开头出现过的主题动机。这个动机里第二小提琴、中提琴和大提琴合奏的几个短促的跳音，笔者认为可能是第四乐章里“叩门动机”的雏形。

紧随其后一段诡异的、迷离的同时也是令人毛骨悚然的半音阶，让笔者联想到《1984》里那个人人自危的极权主义社会。在那里，监控遍布各地，可能随便一位看起来面善的老头就是“思想警察”。每个人都小心翼翼的，生怕说错了话被捉到把柄，然后被关进监狱，送到101房间。扯远了。这段半音阶里，大提琴同时在拉着主旋律——旋律柔美却悲伤，像一个住在过去的人追忆着似水年华。最后是之前出现过的三个主题动机的再现，似是将死之人对过往的总结，但很可惜，过往千疮百孔，痛苦不堪。最后的16小节组成本乐章的尾声，和开头的引子遥遥呼应。整个乐章的调性在g小调和c小调之间切换，最后在长长的、很弱（谱面符号：pp）的升A中结束。

第四乐章：回旋曲式

这个乐章是回旋曲式的结构，有三个主部和两个插部。

以升c小调开始，开头便是三个重音演奏的“叩门动机”——在那个“大清洗”的年代，克格勃不知何时便会敲响你家房门。每个人都在提心吊胆的活着。有一个地狱笑话是这么说的：两个克格勃因为星座的问题争吵不休，于是同时驱车前往一位天文学家的房子打算请教那位天文学家。天文学家看到他们，以为是来逮捕自己的，于是从家里跳了下去，自杀身亡。克格勃见状只能放下争论，开车离开。同时这里又引用了第一大提琴协奏曲开头的四音动机——G(G)E(降F)H(降C)B(降B)。后两个音小二度的不和谐音程本身就非常紧张，重击的叩门声更加剧了这种感觉，似乎随时随地你都可能被克格勃找上门然后被处决。

之后是一段插部。这一段的情绪色彩似乎并没有刚才那样的激烈紧张。刚开始，第二小提琴、第三小提琴和大提琴缓慢拉出一段改编自俄罗斯葬礼歌曲《被囚的痛苦》的旋律，但随后第一小提琴加入的长音却又给这层肃穆庄严蒙上了紧张的色彩，下一场情绪爆发正在酝酿……肖斯塔科维奇的一生何尝不是被苏联高压政治囚禁的一生呢？

GEHB动机和叩门动机又把旋律拉回了主部。叩门声重复了两遍，签名动机将旋律引入了第二个插部，这个插部的主旋律改自苏联革命歌曲《光荣牺牲》。第一大提琴拉着《光荣牺牲》的旋律，而第二小提琴、中提琴和大提琴则拉着长音，整体听起来似是长长的悲叹，哀悼死于战争的百姓们，同时也哀悼自己。

这段插部的后面，大提琴突然在高音部分拉出了《姆岑斯克县的麦克白夫人》里的唱段：《谢辽沙，我的爱人》。这部歌剧对肖斯塔科维奇的人生轨迹影响重大：他差点因为这部歌剧丢了性命。《真理报》严厉批评这部剧，称其为”是混乱而非艺术“，他本人也被批成了”人民公敌“。当时第四交响曲已经写出来了，但受到了这部剧的牵连，无法在公开场合演奏。一年后，他靠着《d小调第五交响曲》翻案。

最后GEHB和叩门动机又把旋律拉回了主部，而DSCH动机则把音乐引向了末乐章。

第五乐章：二部曲式

最后一个乐章又是较慢地广板，由低音部用DSCH这个签名动机引入，同时高音部演奏着主旋律。然后，签名动机给到中音部，低音部拉着主旋律——签名动机又到了高音部（第二小提琴），中音部拉着主旋律——最后是第一小提琴接过签名动机，第二小提琴拉着主旋律。签名动机和主旋律依旧在不同声部里游荡，调性也在c小调、g小调和升c小调间切换。主旋律就像一只折了翼的鸟，在空中挣扎盘旋，却逃不过越飞越低的结局。一段和第一乐章一模一样的密接合应，然后又是第一乐章里出现过的第一交响曲片段，再是之前的主旋律——似是对整个乐章的回望，又可能是对已经走过的人生、已经经历的历史的回望。结束时的长音，似一声轻轻的叹息——那些都过去了，书也该关上了。

整体上看该乐章并没引入新的材料，它和第一乐章遥遥呼应，同时又升华了本部作品的主题。

结语

肖斯塔科维奇和他所处的年代已离我们远去，但透过他的作品，我们却能真真切切地看到那个年代对一个活人的摧残。高压极权下，肖斯塔科维奇感到扭曲和煎熬，这份扭曲又通过他的作品传达给了听众。他不是天生的战士，他也需要表面的妥协换取更大的生存空间；但他的内心，绝不麻木和屈服。他的作品是诚挚的、冷峻的，和他的面相十分相似：一张孩子气的脸，一双大大的眼，还有冷峻犀利的眼神。

---

一份特殊的声明： 这篇文章同时是为浙江大学古典音乐协会写的导赏推文，希望大家到时候能多多关注浙大古协公众号谢谢~

以及感谢古典音乐协会各位前辈的帮助！

---

插值问题

物理问题 $\rightarrow$ 离散化 $\rightarrow$ 计算机处理

离散的物理数据，但不知道实际函数$\rightarrow$ 构造近似函数作为实际函数$f(x)$的逼近

---

插值问题的数学表述： $f(x)$是定义在区间$[a, b]$的函数，$(x_0, y_0),\ (x_1, y_1),\ (x_2, y_2)...,\ (x_n, y_n)$是该区间上$n+1$个不同的点。我们需要构造一个便于计算的函数$P(x)$，s.t.

$$P(x_i) = y_i$$

则称$P(x)$是$f(x)$的插值函数，$[a, b]$是插值区间，$(x_i, y_i)$是插值节点。同时在其他$x \neq x_i$点上，$P(x)$可以作为$f(x)$的近似。

多项式插值

设$P_n(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n,\;\; a_0, a_1, ..., a_n \in \mathbb{R}$

---

定理：对于$n+1$个互不相同的插值节点，满足插值条件的$n$次多项式插值函数存在且唯一。

---

多项式插值方法一 —— 拉格朗日插值法

引入：线性插值

给定两个点$(x_0, y_0)$，$(x_1, y_1)$求解

$$\begin{cases} a_0+ a_1x_0 = y_0\\ a_0+ a_1x_1 = y_1 \end{cases}$$

可得

$$P_1(x) = a_0+ a_1x = \frac{x-x_1}{x_0 - x_1}y_0 + \frac{x-x_0}{x_1 - x_0}y_1$$

推广：拉格朗日插值

$$P_n(x) = \sum_{k=0}^n l_k(x) \cdot y_k, \quad l_k(x) = \prod_{j \neq k} \frac{x - x_j}{x_k - x_j}$$

其中$l_k(x)$被称作基函数。

拉格朗日插值基函数满足以下性质：

• 归一性：$l_k(x_i) = \begin{cases} 1 \quad i = k\\ 0 \quad o/w \end{cases}$
• 多项式次数：每个$l_k$是$n$次多项式。

举例理解

上面的线性插值已经是一个例子。现在看$n = 2$：

对于$(x_0,x_1,x_2)$，

$$\begin{aligned} l_0(x) &= \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} \\ l_1(x) &= \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} \\ l_2(x) &= \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} \end{aligned}$$

线性插值误差

---

定理：设 $f(x)$ 一阶连续可导，且 $f''(x)$ 在区间 $(a, b)$ 上存在，则对任意 $x \in [a, b]$，存在 $\xi \in [a, b]$ 使得：

$$R(x) = f(x) - P_1(x) = \frac{f''(\xi)}{2}(x-x_0)(x-x_1)$$

---

证明过程：

定义误差函数：

$$R(x) = f(x) - P_1(x) = k(x)(x-x_0)(x-x_1)$$

构造辅助函数：

$$\phi(t) = f(t) - P_1(t) - k(x)(t-x_0)(t-x_1)$$

$\phi(t)$ 在 $x_0,x,x_1$ 处有零点，且$\phi'(t)$ 在 $(\xi_1,\xi_2)$ 有零点

$\therefore$ 应用Rolle定理：$\phi''(\xi) = 0$ $\Rightarrow$ $f''(\xi) = 2k(x)$

一般形式的误差估计： 对于 $n$ 次插值多项式 $P_n(x)$：

$$R_n(x) = f(x) - P_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}\omega_{n+1}(x)$$

其中：

$$\omega_{n+1}(x) = \prod_{i=0}^n (x-x_i)$$

$\therefore$

1. 误差与高阶导数 $f^{(n+1)}$ 成正比
2. 节点越密集 ($(x-x_i)$ 越小)，误差越小
3. 增加节点数 $n$ 可提高精度

很多情况下，$f^{(n+1)}$ 未知，可采用以下方法估计：

使用 $n+2$ 个数据点进行两次插值运算：前 $n+1$ 点构造 $P_n(x)$；后 $n+1$ 点构造 $\hat{P}_n(x)$。整理可得误差关系式：

$$f(x) - P_n(x) \approx \frac{x-x_0}{x_0-x_{n+1}}(P_n(x)-\hat{P}_n(x))$$

拉格朗日插值法的优点/缺点：

• 优点：
  • 显示公式：无需解线性方程组，直接构造多项式。
  • 理论直观
• 缺点：
  • 计算效率低：新增节点需重新计算所有基函数。
  • 数值不稳定：高次插值时可能因舍入误差放大失效。

多项式插值方法二——牛顿插值法

引入

避开了拉格朗日插值法“新增节点需重新计算所有基函数”这一问题。

由数学知识可知任何一个多项式都可以表示为：

$$N_n(x) = a_0 + \sum_{k=1}^n a_k \prod_{i=0}^{k-1} (x - x_i)$$

在牛顿形式下，我们可以认为此时$a_k$对应的基函数是$k$的多项式$\prod_{i=0}^{k-1} (x - x_i)$，它们相互独立。因此有更高阶数加入的时候只需计算相应新的多项式系数即可。

计算步骤

将插值条件$P(x_i) = y_i$写成线性方程组的形式：

$\begin{cases} y_0 = a_0 = f(x_0)\\ y_1 = y_0 +a_1 (x_1-x_0) = f(x_1)\\ y_2 = y_0 + a_1 (x_2-x_0) + a_2(x_2-x_0)(x_2-x_1) = f(x_2)\\ ...\\ y_n = y_0 + a_1 (x_n-x_0) + a_2(x_n-x_0)(x_n-x_1) + ... + a_n(x_n-x_0)(x_n-x_1)...(x_n-x_{n-1}) = f(x_n) \end{cases}$
引入差商的概念：
由$(y_0, y_1)$我们引入一阶差商

$$F(x_0, x_1) = \frac{f(x_1) - f(x_0)}{x_1 - x_0}$$

类似可得更高阶的差商公式：

$$F(x_2, x_1) = \frac{f(x_2) - f(x_1)}{x_2 - x_1}\\ F(x_0, x_1,x_2) = \frac{F(x_2, x_1)-F(x_0, x_1)}{x_2-x_0}\\ ...\\ F(x_0,...,x_n) = \frac{F(x_1,...,x_n)-F(x_0,...,x_{n-1})}{x_n-x_0}$$

根据以上公式我们可以改写差商形式的牛顿插值多项式：

$$P_n(x) = F(x_0) + \sum_{k=1}^n F(x_0,...,x_k) \cdot \prod_{i=0}^{k-1}(x-x_i)$$

示例

$$\begin{aligned} P_3(x) = & F(x_0)+ F(x_0,x_1)(x-x_0) \\ & + F(x_0,x_1,x_2)(x-x_0)(x-x_1) \\ & + F(x_0,x_1,x_2,x_3)(x-x_0)(x-x_1)(x-x_2) \end{aligned}$$

牛顿差商的性质

1. 线性性：
   若$h(x) = \alpha f(x) + \beta g(x)$，则：

$$H(x_0,...,x_n) = \alpha F(x_0,...,x_n) + \beta G(x_0,...,x_n)$$

2. 对称性
   差商值与节点排列顺序无关：

$$F(x_0,x_1,...,x_n) = F(x_{\sigma(0)},x_{\sigma(1)},...,x_{\sigma(n)})$$

其中$\sigma$是任意排列

3. 差商和导数关系：
   若$f(x)\in C^n[a,b]$，则存在$\xi\in(a,b)$使得：

4. 差商表可加性：
   新增节点$x_{n+1}$时：

$$F(x_0,...,x_{n+1}) = \frac{F(x_1,...,x_{n+1}) - F(x_0,...,x_n)}{x_{n+1}-x_0}$$

$$F(x_0,...,x_n) = \frac{f^{(n)}(\xi)}{n!}$$

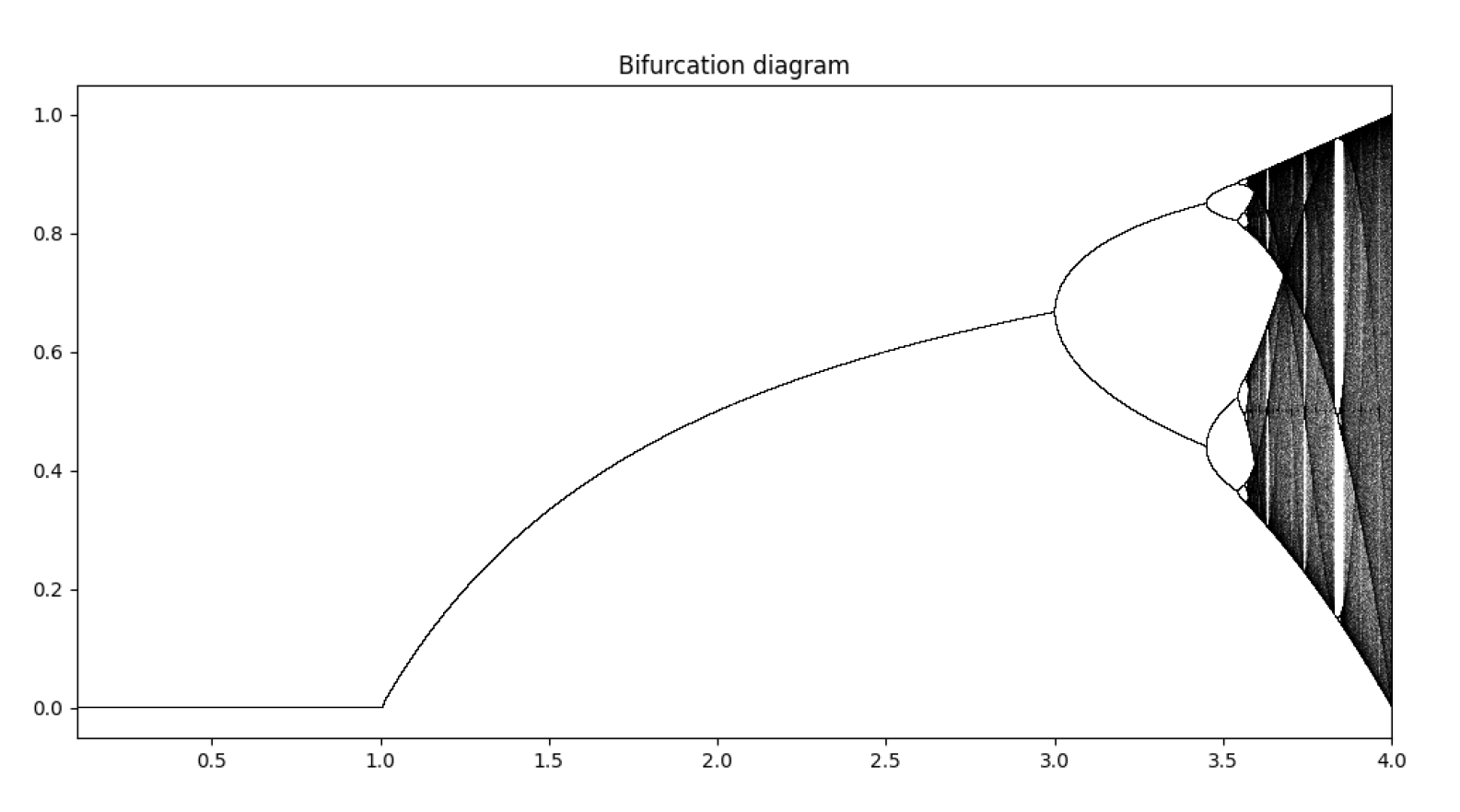
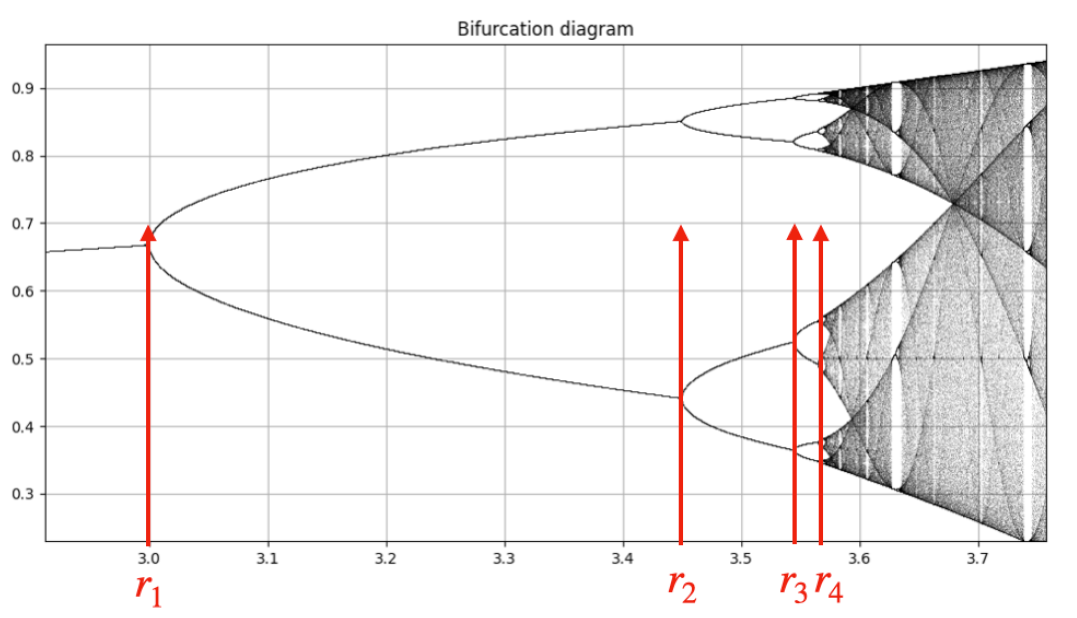
荣格(Runge)现象

指在高次多项式插值中，随着插值节点数量的增加，插值结果在区间端点附近出现剧烈振荡的现象。这种现象由德国数学家Carl Runge在研究多项式插值时首次发现。

解决方法：多次线性插值

将插值区间划分为若干子区间，在每个子区间上用线性多项式进行插值的方法。给定节点$(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$，我们构造的插值函数应该满足：

• $S(x_i) = y_i$ （通过所有节点）
• $S(x)$在每个$[x_i,x_{i+1}]$上是线性函数
• 整体函数连续（$C^0$连续）

具体实现步骤：

1. 找到待插值点$x$及其所在的区间$[x_k,x_{k+1}]$
2. 计算：$ P_1(x) = \frac{x-x_{k+1}}{x_k - x_{k+1}}y_k + \frac{x-x_k}{x_{k+1} - x_k}y_{k+1} $

缺陷：$C^1$不连续

样条插值

样条插值（Spline Interpolation）是一种分段低次多项式插值方法，通过强制拼接点处的光滑条件来保证整体曲线的平滑性。

插值函数需要满足：

• $S_i(x_i)=y_i$, $S_i(x_{i+1})=y_{i+1}$（插值条件）
• 连续性：
  • $C^0$: $S_{i-1}(x_i) = S_i(x_i)$
  • $C^1$: $S'_{i-1}(x_i) = S'_i(x_i)$
  • $C^2$: $S''_{i-1}(x_i) = S''_i(x_i)$

最常用：三次样条插值函数，即在每段$[x_i,x_{i+1}]$上构造：

$$S_i(x) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 + d_i(x-x_i)^3$$

对$n+1$个插值点，总共有$n$个区间，那么总参数有$4n$个。

约束条件：

• 插值条件：提供 $n+1$ 个
• 连续性：提供 $3(n-1)$ 个
• 边界条件：提供n个

对于$x \in [x_k, x_{k+1})$：

$$\begin{aligned} S_k(x) &= a_k + b_k h + c_k h^2 + d_k h^3 \quad (h = x-x_k) \\ S'_k(x) &= b_k + 2c_k h + 3d_k h^2 \\ S''_k(x) &= 2c_k + 6d_k h \end{aligned}$$

应满足条件：

• $S_k(x_k) = y_k \Rightarrow a_k = y_k$
• $ S_k(x_{k+1}) = y_{k+1} \Rightarrow a_k + h_k b_k + h_k^2 c_k + h_k^3 d_k = y_{k+1} $ （其中 $h_k = x_{k+1}-x_k$）
• $ b_k + 2h_k c_k + 3h_k^2 d_k = b_{k+1} $
• $ 2c_k + 6h_k d_k = 2c_{k+1} $

求解该方程组：
令 $m_k = 2c_k$，则：

1. 由二阶导数连续条件：

   $$d_k = \frac{m_{k+1}-m_k}{6h_k}$$

2. 代入插值方程得：

   $$b_k = \frac{y_{k+1}-y_k}{h_k} - \frac{h_k}{2}m_k - \frac{h_k}{6}(m_{k+1}-m_k)$$

3. 将系数代入一阶导数连续条件，得到：

$$h_k m_k + 2(h_k+h_{k+1})m_{k+1} + h_{k+1}m_{k+2} = 6\left(\frac{y_{k+2}-y_{k+1}}{h_{k+1}} - \frac{y_{k+1}-y_k}{h_k}\right)$$

4. 将上两个边界条件的约束 $\Rightarrow$ 建立起线性方程组即可求解。

数据拟合

数据拟合是通过数学模型近似描述离散数据点的方法，与插值的区别在于：

• 插值：强制通过所有数据点
• 拟合：允许存在偏差，追求整体趋势匹配

最小二乘法拟合

数学原理：最小化残差平方和：

$$\min \sum_{i=1}^n (y_i - f(x_i))^2$$

线性拟合：

考虑$f(x) = a + bx$。
残差平方和：$$Q(a,b) = \sum_{i=1}^n (f(x_i) - y_i)^2 = \sum_{i=1}^n (a + b x_i - y_i)^2$$
$Q(a, b)$最小，需满足：

$$\begin{cases} \frac{\partial Q}{\partial a} = 2\sum_{i=1}^n (a + b x_i - y_i) = 0\\ \frac{\partial Q}{\partial b} = 2\sum_{i=1}^n (a + b x_i - y_i)x_i = 0 \end{cases}$$

将方程组整理为矩阵形式：

$$\begin{bmatrix} n & \sum x_i \\ \sum x_i & \sum x_i^2 \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \end{bmatrix}$$

求解$(a, b)$即可。

多项式拟合

k次多项式模型：

$$f(x) = \sum_{j=0}^k a_j x^j$$

残差平方和：

$$\begin{cases} a_0 \sum 1 + a_1 \sum x_i + \cdots + a_m \sum x_i^m = \sum y_i \\ a_0 \sum x_i + a_1 \sum x_i^2 + \cdots + a_m \sum x_i^{m+1} = \sum x_i y_i \\ \vdots \\ a_0 \sum x_i^m + a_1 \sum x_i^{m+1} + \cdots + a_m \sum x_i^{2m} = \sum x_i^m y_i \end{cases}$$

整理成矩阵形式：

$$\begin{bmatrix} n & \sum x_i & \cdots & \sum x_i^m \\ \sum x_i & \sum x_i^2 & \cdots & \sum x_i^{m+1} \\ \vdots & \vdots & \ddots & \vdots \\ \sum x_i^m & \sum x_i^{m+1} & \cdots & \sum x_i^{2m} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_m \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \\ \vdots \\ \sum x_i^m y_i \end{bmatrix}$$

求解即可。

非线性拟合

模型类型	变换方法	线性形式
指数模型 $y=ae^{bx}$	取对数	$\ln y = \ln a + bx$
幂函数 $y=ax^b$	取对数	$\ln y = \ln a + b\ln x$
对数模型 $y=a\ln x + b$	-	直接拟合
倒数模型 $y = \frac{x}{a+bx}$	取倒数	$\frac{1}{y} = \frac{a}{x} + b$

容易出现的问题：欠拟合&过拟合。

数值微分

用离散点进行数值微分：

假设数据点均匀分布，$x_i = x_0 + i \cdot h$，在$x_{i-1}$、$x_i$、$x_{i+1}$附近Taylor展开：

$$f_{i+1} = f_i + h f'_i + \frac{h^2}{2} f''_i + \frac{h^3}{6} f'''_i + O(h^4)$$

$$f_{i-1} = f_i - h f'_i + \frac{h^2}{2} f''_i - \frac{h^3}{6} f'''_i + O(h^4)$$

就可以得到以下公式：

类型	公式	误差阶
前向差分	$f'(x) \approx \frac{f(x+h)-f(x)}{h}$	$O(h)$
后向差分	$f'(x) \approx \frac{f(x)-f(x-h)}{h}$	$O(h)$
中心差分	$f'(x) \approx \frac{f(x+h)-f(x-h)}{2h}$	$O(h^2)$

再在$x_{i-2}$、$x_{i+2}$处展开：

$$f_{i+2} = f_i + 2h \cdot f_i' + \frac{4h^2}{2!} f_i'' + \frac{8h^3}{3!} f_i'''+...$$

$$f_{i-2} = f_i - 2h \cdot f_i' + \frac{4h^2}{2!} f_i'' - \frac{8h^3}{3!} f_i'''+...$$

又 $\because$

$$f_{i+1} = f_i + h f'_i + \frac{h^2}{2} f''_i + \frac{h^3}{6} f'''_i + O(h^4)$$

$$f_{i-1} = f_i - h f'_i + \frac{h^2}{2} f''_i - \frac{h^3}{6} f'''_i + O(h^4)$$

消去$f_i'''$，可得：

数值积分

数据滤波

前言

“混沌”系统和随机过程的本质区别：

• 真随机过程完全不可预测，我们可能知道其概率分布，但是对于系统演化中特定时间的单次结果无法进行判断；
• 混沌系统的本质仍是确定过程，不过由于精确的解析解无法求得，或者计算过程中存在误差，使得结果的误差和计算复杂度急剧上升，导致对未来的状态无法提前预判。

从线性到非线性系统

线性函数（或映射）应该满足叠加性和齐次性，用数学语言表述，

$$f(\alpha x+ \beta y) = \alpha f(x) + \beta f(y)$$

由线性函数决定的系统称为线性系统。

数理方法中接触到的Poisson方程、波动方程、热传导方程均满足上述性质。

但不是所有的方程都满足线性性（废话，这显然）。举一个例子：

$$\frac{du}{dt} = u^2$$

就不满足。

插入一张课件里出现的表格，描述自由度和非线性程度之间的联系：

根据描述系统的动力学方程进行分类：

• 迭代映射：离散时间的问题，通过迭代决定系统的演化：$x_{n+1} = f(x_n)$
• 微分方程：连续时间的问题，通过微分方程决定系统的演化。形式常为：

$$\dot x_1 = f_1(x_1, x_2, ..., x_n)\\ \dot x_2 = f_2(x_1, x_2, ..., x_n)\\ \vdots\\ \dot x_n = f_n(x_1, x_2, ..., x_n)$$

离散的迭代映射

离散的迭代映射用于研究非线性过程可以直观揭示其中的混沌演化过程。它也是我们之前用于微分方程差分离散化后的形式。

特点：

• 离散过程广泛存在于各种自然现象，比如数字电子学、机械系统、经济金融学等
• 离散过程用于研究非线性过程可以直观揭示其中的混沌演化过程

不动点

不动点满足$x^* = f(x^*)$。
如果达到不动点，那么$x_{n+1}$和$x_{n}$的迭代不再发生变化，系统演化已达到稳定。

不动点是一个函数映射到自身的一个点，可以用来描述系统的平衡和稳定。在物理学的相变理论中，可以分析靠近不稳定的不动点来研究临界现象。

不动点的稳定性：

一个动力学系统可能有多个不动点，但各个不动点的稳定性可能截然不同。

为了分析不动点的稳定性，我们可以在不动点附近做一个扰动，$x_n = x^* + \eta_n$，迭代之后，利用关系式$x_{n+1} = f(x_n)$：

$$x_{n+1} = f(x_n) = f(x^* + \eta_n) = f(x^*) + f'(x^*)\eta_n + O(\eta^2 _n)$$

其中最后一个等号用到了泰勒展开。根据$x_{n+1} = x^* + \eta_{n+1}$，再加上不动点的定义，我们有：

$$\begin{array}{c} x_{n+1} = x^* + \eta_{n+1} = f(x_n) = f(x^* + \eta_n) = f(x^*) + f'(x^*)\eta_n + O(\eta^2 _n)\\ \\ \Rightarrow \eta_{n+1} \approx f'(x^*)\eta_n \end{array}$$

对于不动点$x^*$，扰动之后是否继续回到不动点取决于$\lambda = f'(x^*)$的值：

1. $|\lambda|<1$：不动点稳定
2. $|\lambda|>1$：不动点不稳定，系统将逐渐偏离不动点
3. $|\lambda|=1$：分析高阶的$\eta_n$特征进一步判断

(A tip prepared for myself: 上述结论和比值判定法判别级数收敛性很相似。可以对比记忆？)

e.g. 对于迭代映射：$x_{n+1} = x_n$，求解其不动点$x^* = (x^*)^2$，可得分别有解$x^* = 0$ 和 $x^* = 1$。

为了分析不动点的稳定性，利用上面结论，求$\lambda = f'(x^*) = 2x^*$：

• 不动点$x^* = 0$，$\lambda = 0 < 1$：稳定的不动点
• 不动点$x^* = 1$，$\lambda = 2 > 1$：不稳定的不动点

蛛网图： 可以直观的表示出不动点及其稳定性和周期性的特征。通过从初始点开始做迭代关系式的交点，然后根据新的迭代值取直线$y = x$的交点，循环往复，我们可以得到不动点附近扰动所带来新的变化趋势。

e.g.
（这里的备注文字容我再思考一会……）

逻辑斯蒂 (Logistic) 映射

对上述例子的映射再添加一个线性映射$x_{n+1} = r x_n$项得到。

逻辑斯蒂方程 (Logistic Equation) 介绍：
逻辑斯蒂方程 (Logistic Equation) 是描述生物数量增长的一个合理模型。它的离散形式可以写成：

$$x_{n+1} = r x_n (1-x_n)$$

这里$x_n$是第$n$次迭代的取值。增长率$r$决定了系统演化的特征。

从迭代格式中我们可以设定变量的范围：$0<x_i<1$，并且在$x_i = \frac{1}{2}$时取得最大值。将$x_i = \frac{1}{2}$代入上式：

$$r = \frac{x_{n+1}}{x_n (1-x_n)}\\ \Rightarrow r_{max} = \frac{1}{\frac{1}{2} \cdot \frac{1}{2}} = 4$$

因此可以限制增长率的变化范围：$0 \leqslant r \leqslant 4$。

同时易得逻辑斯蒂方程的两个不动点：$x^* = 0$和$x^* = 1 - \frac{1}{r}$；对于不同的初始值$x_0$和增长率$r$，我们可以通过计算得到系统演化的结果。

逻辑斯蒂方程迭代

下面展示几个$r$值对系统的影响：
$r\leqslant 3.0$：

$3.0 < r \leqslant r_3\approx 3.5$：

$r>r_3 \approx 3.5$：

不定点数量、取值与$r$大小之间的关系——分叉图：

先对分叉图进行定性讨论：

• $r<1$：趋于灭绝，即经过足够多的迭代之后，$x_n \rightarrow 0$。
• $1 <r\leqslant 3$：趋于定态，即经过足够数量的迭代之后，$x_n$固定在一个确定的值上定值则由$r$确定。
• $3 <r\approx 3.5$：周期变化，开始分叉时以2为周期，后又以4为周期。
• $r>r_3 \approx 3.5$：混沌态，轨迹点永不重复，不进入任何周期状态。
• $r \in (r_4 \approx 3.83, r_5 \approx 3.86)$：系统会从混沌状态回到短暂的周期性，并且紧接着又回到混沌状态。此时的周期数为3的倍数。

（至于为什么$r_3, r_4, r_5$等于上面的三个数值，后面有数学证明。）

---

理解分叉：

• 前两种状态比较好理解：分别对应蛛网图和折线图的前两张。
• 周期分叉的出现（当 $( r > 3.0 )$ 时）：由于周期性的存在，设系统存在的两个周期点分别为$p$ 和 $q$，满足：

  $$f(p) = q, \quad f(q) = p$$

  那么系统演化到这两点时将进入周期模式。
  同时我们可以通过方程$f(f(x)) = x$ 求解这两个周期点：

  $$r[x(1 - x)] [1 - rx(1 - x)] = x$$

  这是一个四次多项式方程，除去不动点 $x_1^*$ 和 $x_2^*$ 后，剩余两个解为：

  $$p, q = \frac{r + 1 \pm \sqrt{(r - 3)(r + 1)}}{2r}$$

  $\therefore$ 当 $r > 3$ 时，系统开始出现2周期解，即分叉现象。
  考察 $f(f(x))$ 在 $p$ 和 $q$ 处的导数：

  $$\lambda = \frac{d}{dx} f(f(x)) = r(1 - 2q) \cdot r(1 - 2p) = r^2 [1 - 2(p + q) + 4pq]$$

  化简后得到：

  $$\lambda = -r^2 + 2r + 4$$

  $\therefore$ 当 $|\lambda| < 1.0$ 时，2周期解是稳定的，对应的参数范围为：

  $$3.0 < r < 1 + \sqrt{6} \approx 3.4494897$$

李雅普诺夫 (Lyapunov) 指数

当存在更多周期性，以至于趋于无穷多周期性时，我们应当如何定量刻画“混沌”？——李雅普诺夫指数。

定义：
从给定的$x_0$初值，以及它附近的一个扰动$\delta_0$，经过多次迭代之后，在$x_n$处存在一个偏离$\delta_n$，那么我们可以用关系式

$$|\delta_n| =|\delta_0|e^{n\lambda}$$

衡量。其中$\lambda$即为李雅普诺夫 (Lyapunov) 指数。容易发现，当$\lambda$为正数时，初值的敏感性极强，会发生混沌。

Calculation：
从 $\lambda$ 的定义出发，我们有：

$$\lambda = \frac{1}{n} \ln \left| \frac{\delta_n}{\delta_0} \right| = \frac{1}{n} \ln \left| \frac{f^n(x_0 + \delta_0) - f^n(x_0)}{\delta_0} \right|$$

可以表示为导数的形式：

$$\lambda = \frac{1}{n} \ln \left| (f^n)'(x_0) \right|$$

将李雅普诺夫指数进一步展开，可以得到：

$$\lambda = \frac{1}{n} \ln \prod_{i=0}^{n-1} |f'(x_i)| = \frac{1}{n} \sum_{i=0}^{n-1} \ln |f'(x_i)|$$

其中，$x_i$ 是每次迭代的结果。通过累加每次迭代的 $\ln |f'(x_i)|$，可以计算出李雅普诺夫指数。

• $\lambda < 0.0$：系统处于定态或周期态。
• $\lambda > 0.0$：系统趋于混沌状态。

定量普适性： 在分叉图中，除了得到表征混沌出现的李雅普诺夫指数外，我们同样可以发现，开始发生分叉的r值点之间的相对间距有固定比例，我们可以通过计算Feigenbaum常数$\delta$来定量化描述这一特征：

$$\delta = \frac{r_n-r_{n-1}}{r_{n+1}-r_n} \approx 4.6692016...$$

易知和$\pi$、$e$一样，Feigenbaum常数也是一个普适的常数。

再看初值敏感性：
我们现在回过头来看初值敏感性：初值敏感性的存在是混沌中最重要的特征，由于无法精确地确定处置，比如由于实验测量误差或者计算中舍入和截断误差的存在，是的近似相同的初始值，在经过足够多的迭代之后，给出了完全不相同、看似随机的结果。因此又被通俗地称作“蝴蝶效应”——德克萨斯的蝴蝶扇动翅膀可能会引发一场龙卷。

线性微分方程

离散的差分$\rightarrow$连续的微分

e.g. Logistic Equation的微分形式：

$$\dot{X} = rN(1-\frac{N}{K})$$

对比离散形式：$x_{n+1} = r x_n (1-x_n)$，$\therefore$ 不动点意味着$x^* = r x^* (1-x^*)$，即如果$x_n = x^*$，则$x_{n+1} = x_n$。

$$\therefore x_{n+1} - x_n = 0$$

微分形式又可写成：

$$\Delta X = rN(1-\frac{N}{K}) \Delta t$$

$$\therefore \dot X = 0 \Rightarrow \frac{\Delta X}{\Delta t} = 0 \Rightarrow \Delta X = 0$$

可知与差分形式等价。（用到了海涅定理？这个不大确定sry……）

由上可以引出一维下不动点的定义：
如果$\dot x = f(x^*) = 0$，则$x^*$是该系统的不动点。

所以不动点即是非线性方程$f(x) = 0$的零点，它可能有多个解（即存在多个不动点）。

不动点的稳定性

对于每个不动点：

1. 可以从几何的角度去理解稳定性：根据它左右区域的正负来判断。

• $f(x)>0$：向右流动
• $f(x)<0$：向左流动
  如果左右合流：该点稳定；左右分离：该点不稳定。

2. 可以通过偏离不动点之后的变化特征来判断稳定性：假设不动点$x^*$附近有一个扰动$\eta(t)$，那么对应$x(t) = x^* + \eta(t)$的动力学方程为：

$$\frac{d}{dt}(x^*+\eta(t)) = f(x^*+\eta)$$

对右侧进行泰勒展开：

$$f(x^*+\eta) = f(x^*) + f'(x^*)\eta + O(\eta^2) \\ \Rightarrow \dot \eta = f'(x^*)\eta$$

• $f'(x^*)>0$：扰动随时间指数放大 $\Rightarrow$ 不动点不稳定
• $f'(x^*)<0$：扰动随时间指数缩小 $\Rightarrow$ 不动点稳定
• $f'(x^*)=0$：需要对更高阶$\eta^2$进行分析

e.g. 对于动力学方程$\dot x = rx - x^3$，$r$取值不同，（实数域上）不动点数目及其稳定性不同：

• $r \leqslant 0$：仅有一个不动点，该不动点是稳定的。
• $r > 0$：它有三个不动点，$r = 0$、$r = \pm \sqrt r$。其中后两个是稳定不动点。

$\therefore$ 微分方程的参数发生变化时，系统不动点的状态也会发生变化。其中显著的现象就是分叉的出现。如下图所示。

多参数下的分叉和灾变

从上述例子可以看到，针对一个参数r时，当r取值不同方程不动点的稳定性也存在极大的不同，如果我们有多个参数，那么不动点的依赖情况又是什么情形？

例如，在上面的方程里多加一个常数项，$\dot x = h + rx - x^3$。对于不同的$r$和$h$值，其不动点的参数组合空间会更多。

灾变：当系统包含多个参数时，参数变化可能导致系统行为发生突然的、非连续的剧变，这种现象称为 “灾变”(Catastrophe)。

考虑上面非线性系统，当参数$h=0.1$时，其不动点分布如下图所示：

• 红色点：稳定不动点（吸引子）
• 黑色点：不稳定不动点（鞍点或排斥子）

假设系统初始位于右下段的稳定态（红色点），当控制参数$r$变化到$r_c$时，系统行为会发生突变：

• 临界点处：原有稳定不动点与不稳定不动点碰撞（鞍结分岔）
• 灾变发生：系统状态不连续跳跃至左上段的另一稳定态

二维非线性系统

二维动力学方程：

$$\begin{cases} \dot x_1 = f_1(x_1, x_2)\\ \dot x_2 = f_2(x_1, x_2) \end{cases}$$

此时$(x_1, x_2)$就在相空间组成了一条随时间变化的轨迹曲线，而这种轨迹有多种可能性：

• 系统区域一个不动点$x^*$，但稳定性未知
• 轨迹组成一个周期性闭合轨道，$x(t+T) = x(t)$
• 在上面二者之间变化，无法预知

---

存在唯一性定理：

设一阶微分方程组：

$$\frac{d\mathbf{x}}{dt} = \mathbf{f}(\mathbf{x},t), \quad \mathbf{x}(t_0) = \mathbf{x}_0$$

其中 $\mathbf{x} \in \mathbb{R}^n$，$\mathbf{f} = (f_1,...,f_n)^T$ 满足：

1. 连续性条件：$f_i(\mathbf{x},t)$ 在域 $D \subset \mathbb{R}^n \times \mathbb{R}$ 上连续
2. 利普希茨条件(Lipticz)：存在常数 $L>0$，使得 $\forall (\mathbf{x},t), (\mathbf{y},t) \in D$：

   $$\|\mathbf{f}(\mathbf{x},t) - \mathbf{f}(\mathbf{y},t)\| \leq L\|\mathbf{x} - \mathbf{y}\|$$

那么将有下面结论：

1. 解的存在唯一性：在某个区间 $|t - t_0| \leq h$ 上存在唯一解 $\mathbf{x}(t)$
2. 轨道不相交性：若 $\mathbf{x}_1(t_0) \neq \mathbf{x}_2(t_0)$，则 $\forall t$ 有 $\mathbf{x}_1(t) \neq \mathbf{x}_2(t)$

---

考虑非线性动力系统：

$$\begin{cases} \dot x = f(x, y)\\ \dot y = g(x, y) \end{cases}$$

假设$x^*,\ y^*$是它的不动点，即满足：

$$f(x^*, y^*) = 0;\ g(x^*, y^*) = 0$$

在不动点附近加一个$u(t), v(t)$扰动,此时关于扰动的方程可以写成：

$$\begin{cases} \begin{aligned} \dot{u} &= \frac{\partial f}{\partial x} u + \frac{\partial f}{\partial y} v \\ \dot{v} &= \frac{\partial g}{\partial x} u + \frac{\partial g}{\partial y} v \end{aligned} \end{cases}$$

那么我们只需要关注它的Jacobbi矩阵的特征值。（很ODE的感觉……）
它的Jacobbi矩阵

$$A = \begin{pmatrix} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\ \frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{pmatrix}$$

易知它有两个特征值$\lambda_1$、$\lambda_2$。

$\Rightarrow$

类型	特征值条件	相空间行为
排斥子	$\text{Re}(\lambda_1), \text{Re}(\lambda_2) > 0$	所有轨道远离平衡点
吸引子	$\text{Re}(\lambda_1), \text{Re}(\lambda_2) < 0$	所有轨道趋向平衡点
鞍点	$\text{Re}(\lambda_1) \cdot \text{Re}(\lambda_2) < 0$	有进有出（稳定与不稳定流形）
中心	$\lambda_1, \lambda_2 = \pm i\omega$ （纯虚数）	轨道形成闭合环

图示：

和ODE之间的区别：
（思考措辞ing）

Lotka-Volterra模型：

经典的二维非线性系统。非线性项：$xy$。设简化后的方程如下：

$$\begin{cases} \dot x = x(3-x-2y)\\ \dot y = y(2-x-y) \end{cases}$$

给定非线性系统，求得四个不动点坐标为：

$$(x^*, y^*) = (0, 0), \quad (3, 0), \quad (0, 2), \quad (1, 1)$$

系统的雅可比矩阵为：

$$A = \begin{pmatrix} 3 - 2x - 2y & -2x \\ -y & 2 - x - 2y \end{pmatrix}$$

分析不动点稳定性：

1. 不动点 $(0, 0)$

$$A(0,0) = \begin{pmatrix} 3 & 0 \\ 0 & 2 \end{pmatrix}$$

解得特征值：$\lambda_1 = 3$, $\lambda_2 = 2$，两个特征值实部均为正
$\therefore$ 稳定性：排斥子 (不稳定结点)

2. 不动点 (3, 0)

$$A(3,0) = \begin{pmatrix} 3 - 6 & -6 \\ 0 & 2 - 3 \end{pmatrix} = \begin{pmatrix} -3 & -6 \\ 0 & -1 \end{pmatrix}$$

特征值：$\lambda_1 = -3$, $\lambda_2 = -1$，两个特征值实部均为负
$\therefore$ 吸引子 (稳定结点)

3. 不动点 (0, 2)

$$A(0,2) = \begin{pmatrix} 3 - 4 & 0 \\ -2 & 2 - 4 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ -2 & -2 \end{pmatrix}$$

特征值：$\lambda_1 = -1$, $\lambda_2 = -2$，两个特征值实部均为负
$\therefore$ 吸引子 (稳定结点)

4. 不动点 (1, 1)

$$A(1,1) = \begin{pmatrix} 3 - 2 - 2 & -2 \\ -1 & 2 - 1 - 2 \end{pmatrix} = \begin{pmatrix} -1 & -2 \\ -1 & -1 \end{pmatrix}$$

特征值：
$=\lambda = -1 \pm \sqrt{2}$，特征值实部一正一负 $\Rightarrow$ 鞍点
图示如下：

Lorentz方程

洛伦兹在1963年研究大气对流流动的动力学模型中得到的三维系统，其中非线性项主要来自$xy$和$xz$的耦合：

$$\begin{cases} \dot x = \sigma(y-x)\\ \dot y = rx - y -xz\\ \dot z = xy-bz \end{cases}$$

性质：

• 对称性：
  系统在坐标反演变换下保持不变：

$$(x, y, z) \rightarrow (-x, -y, -z), \ f(x, y, z) = f(-x, -y, -z)$$

• 收缩性：
  洛伦兹系统是严格耗散的，相空间体积随时间指数收缩：
  • 体积变化率：

  $$\dot{V} = \nabla \cdot \vec{f} = -\sigma - 1 - b < 0$$

  • 物理意义：

  $$\lim_{t \to \infty} V(t) = V(0)e^{(\nabla \cdot \vec{f})t} \rightarrow 0$$

  所有轨迹最终收缩到零体积集合（吸引子）。
• 非周期性：由收缩性直接得出。反证法：假如存在周期性，那么最终系统将落入一个固定范围的相空间中，与它的收缩性是矛盾的。

分形