前言
“混沌”系统和随机过程的本质区别:
- 真随机过程完全不可预测,我们可能知道其概率分布,但是对于系统演化中特定时间的单次结果无法进行判断;
- 混沌系统的本质仍是确定过程,不过由于精确的解析解无法求得,或者计算过程中存在误差,使得结果的误差和计算复杂度急剧上升,导致对未来的状态无法提前预判。
从线性到非线性系统
线性函数(或映射)应该满足叠加性和齐次性,用数学语言表述,
f(αx+βy)=αf(x)+βf(y)
由线性函数决定的系统称为线性系统。
数理方法中接触到的Poisson方程、波动方程、热传导方程均满足上述性质。
但不是所有的方程都满足线性性(废话,这显然)。举一个例子:
dtdu=u2
就不满足。
插入一张课件里出现的表格,描述自由度和非线性程度之间的联系:
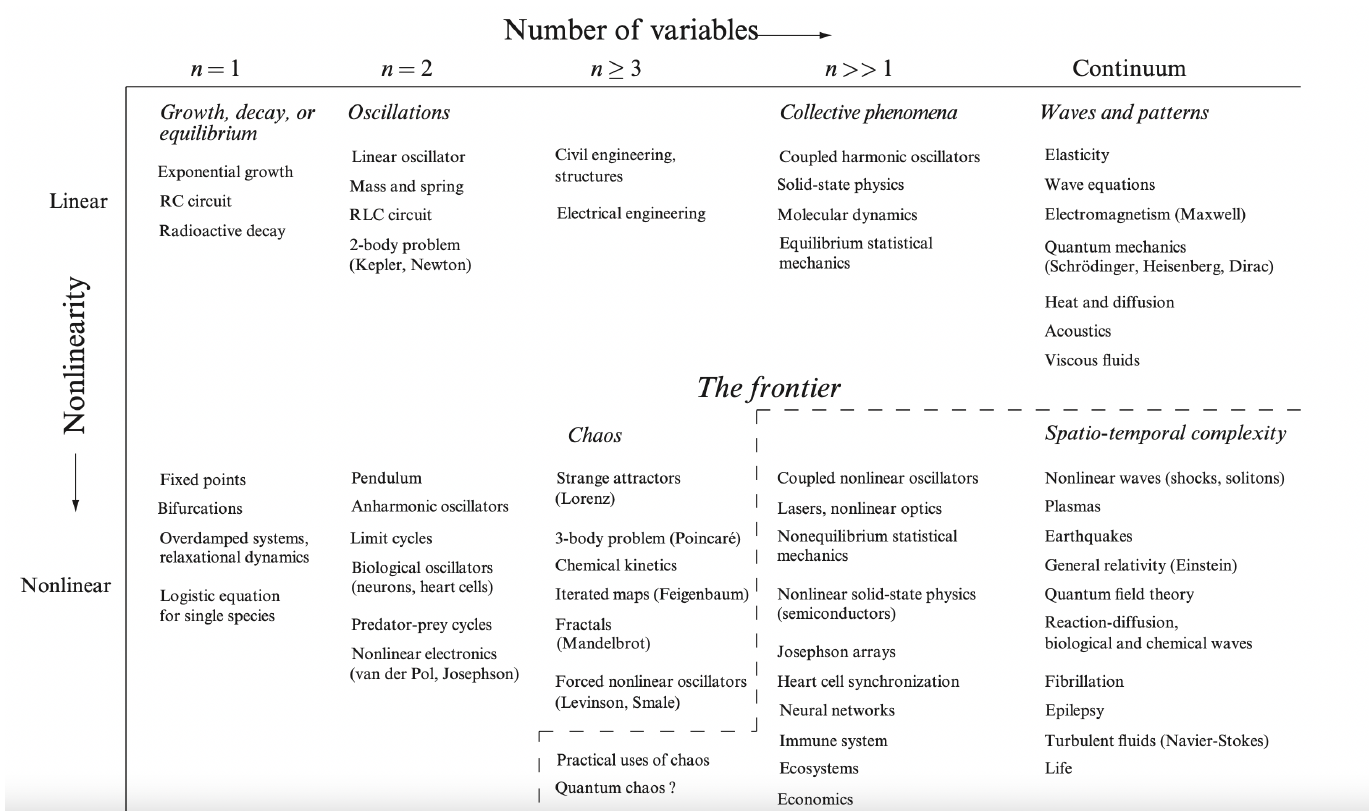
根据描述系统的动力学方程进行分类:
- 迭代映射:离散时间的问题,通过迭代决定系统的演化:xn+1=f(xn)
- 微分方程:连续时间的问题,通过微分方程决定系统的演化。形式常为:
x˙1=f1(x1,x2,...,xn)x˙2=f2(x1,x2,...,xn)⋮x˙n=fn(x1,x2,...,xn)
离散的迭代映射
离散的迭代映射用于研究非线性过程可以直观揭示其中的混沌演化过程。它也是我们之前用于微分方程差分离散化后的形式。
特点:
- 离散过程广泛存在于各种自然现象,比如数字电子学、机械系统、经济金融学等
- 离散过程用于研究非线性过程可以直观揭示其中的混沌演化过程
不动点
不动点满足x∗=f(x∗)。
如果达到不动点,那么xn+1和xn的迭代不再发生变化,系统演化已达到稳定。
不动点是一个函数映射到自身的一个点,可以用来描述系统的平衡和稳定。在物理学的相变理论中,可以分析靠近不稳定的不动点来研究临界现象。
不动点的稳定性:
一个动力学系统可能有多个不动点,但各个不动点的稳定性可能截然不同。
为了分析不动点的稳定性,我们可以在不动点附近做一个扰动,xn=x∗+ηn,迭代之后,利用关系式xn+1=f(xn):
xn+1=f(xn)=f(x∗+ηn)=f(x∗)+f′(x∗)ηn+O(ηn2)
其中最后一个等号用到了泰勒展开。根据xn+1=x∗+ηn+1,再加上不动点的定义,我们有:
xn+1=x∗+ηn+1=f(xn)=f(x∗+ηn)=f(x∗)+f′(x∗)ηn+O(ηn2)⇒ηn+1≈f′(x∗)ηn
对于不动点x∗,扰动之后是否继续回到不动点取决于λ=f′(x∗)的值:
- ∣λ∣<1:不动点稳定
- ∣λ∣>1:不动点不稳定,系统将逐渐偏离不动点
- ∣λ∣=1:分析高阶的ηn特征进一步判断
(A tip prepared for myself: 上述结论和比值判定法判别级数收敛性很相似。可以对比记忆?)
e.g. 对于迭代映射:xn+1=xn,求解其不动点x∗=(x∗)2,可得分别有解x∗=0 和 x∗=1。
为了分析不动点的稳定性,利用上面结论,求λ=f′(x∗)=2x∗:
- 不动点x∗=0,λ=0<1:稳定的不动点
- 不动点x∗=1,λ=2>1:不稳定的不动点
蛛网图: 可以直观的表示出不动点及其稳定性和周期性的特征。通过从初始点开始做迭代关系式的交点,然后根据新的迭代值取直线y=x的交点,循环往复,我们可以得到不动点附近扰动所带来新的变化趋势。
e.g. 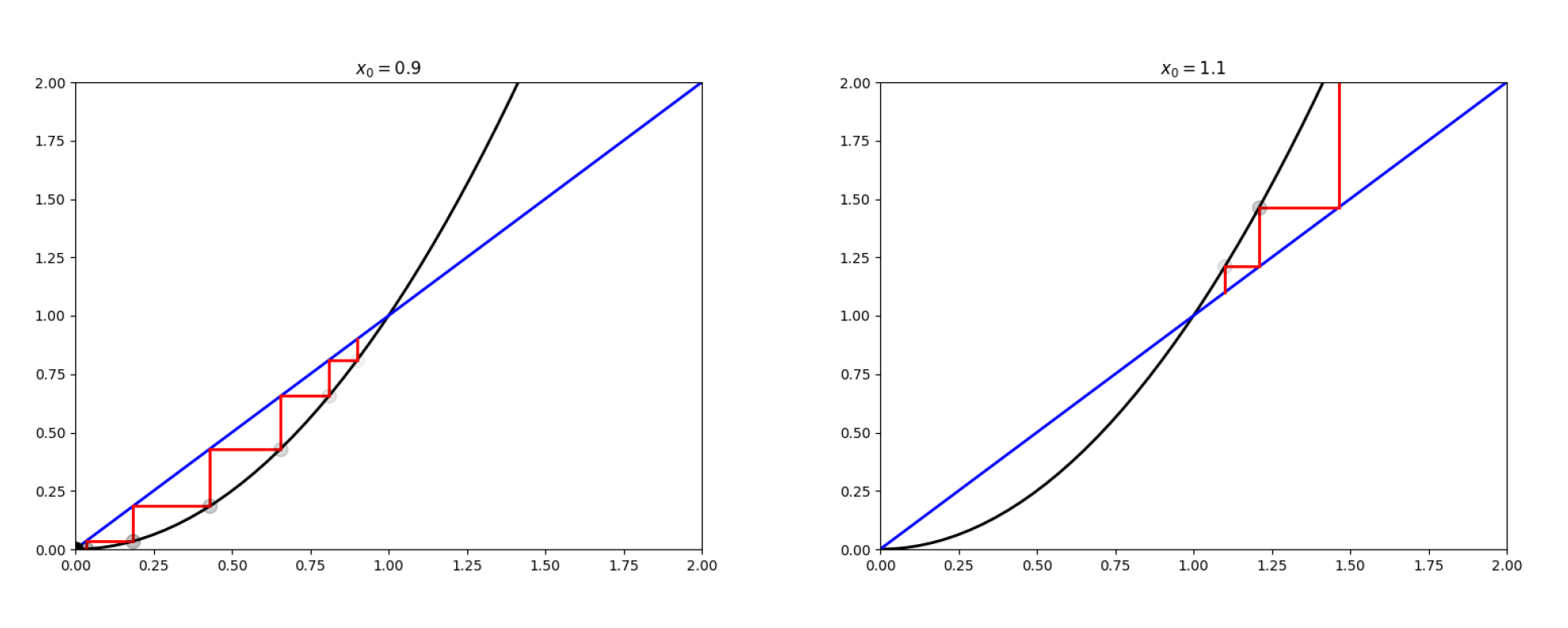
(这里的备注文字容我再思考一会……)
逻辑斯蒂 (Logistic) 映射
对上述例子的映射再添加一个线性映射xn+1=rxn项得到。
逻辑斯蒂方程 (Logistic Equation) 介绍:
逻辑斯蒂方程 (Logistic Equation) 是描述生物数量增长的一个合理模型。它的离散形式可以写成:
xn+1=rxn(1−xn)
这里xn是第n次迭代的取值。增长率r决定了系统演化的特征。
从迭代格式中我们可以设定变量的范围:0<xi<1,并且在xi=21时取得最大值。将xi=21代入上式:
r=xn(1−xn)xn+1⇒rmax=21⋅211=4
因此可以限制增长率的变化范围:0⩽r⩽4。
同时易得逻辑斯蒂方程的两个不动点:x∗=0和x∗=1−r1;对于不同的初始值x0和增长率r,我们可以通过计算得到系统演化的结果。
逻辑斯蒂方程迭代
下面展示几个r值对系统的影响:
r⩽3.0:
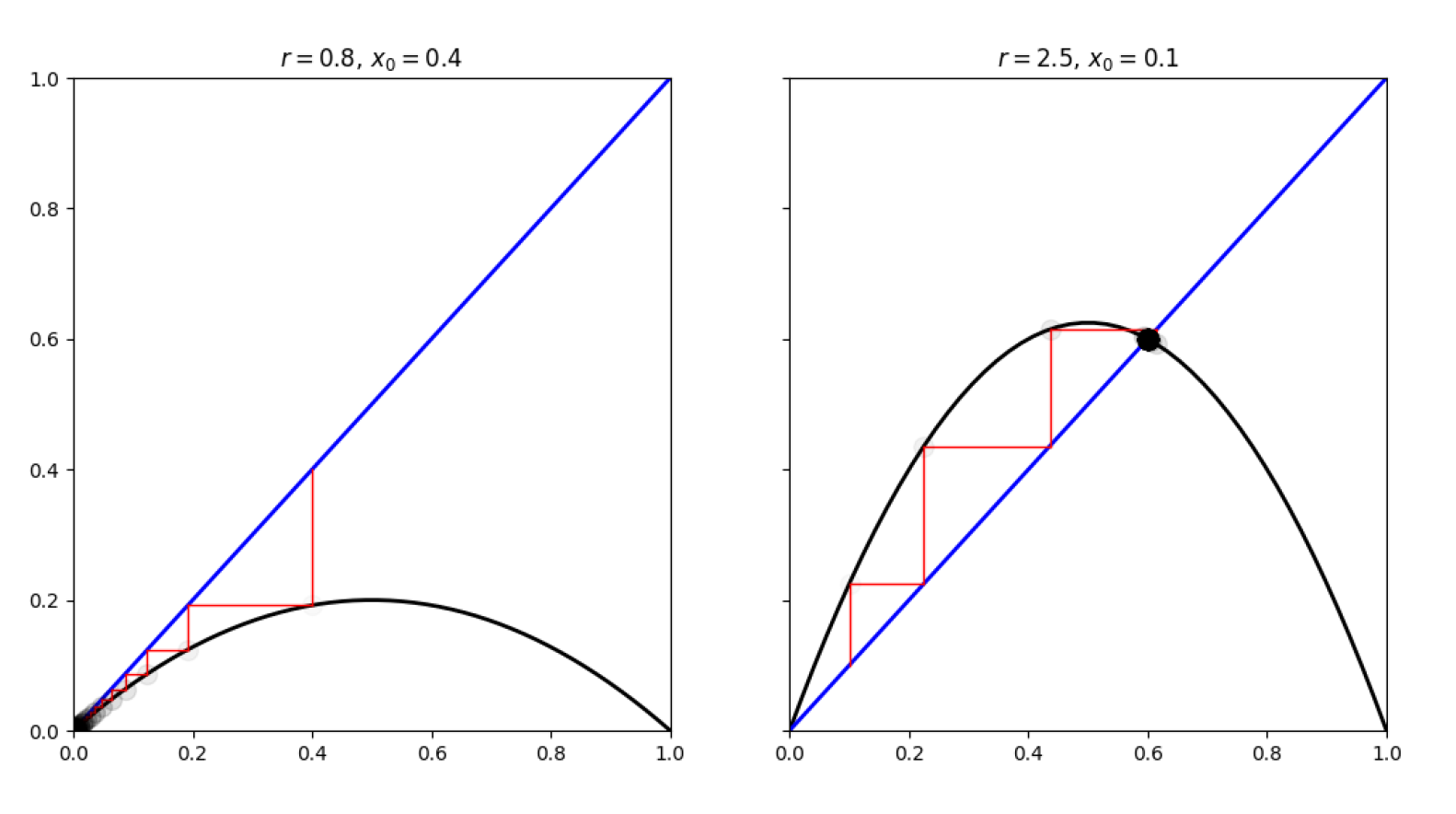
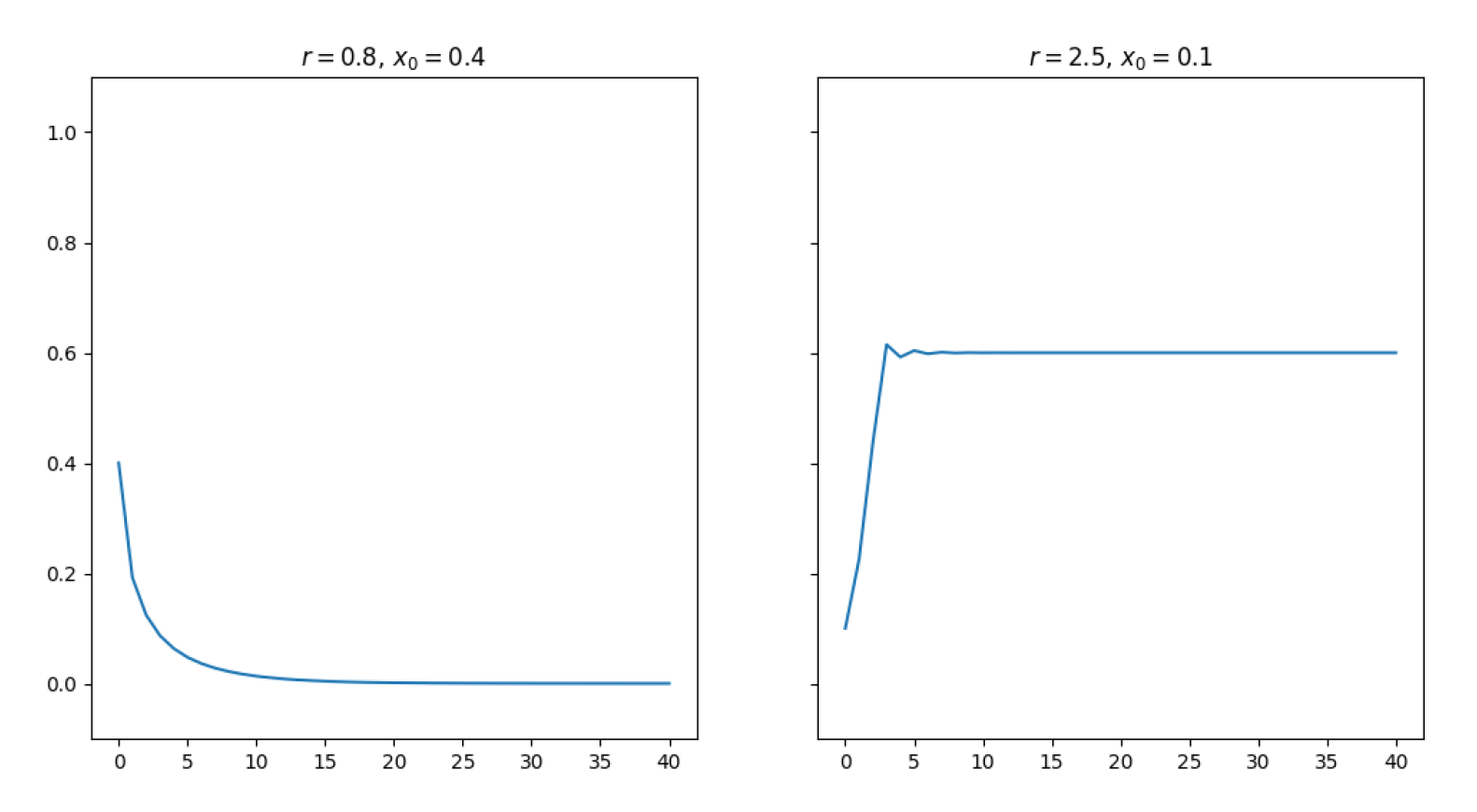
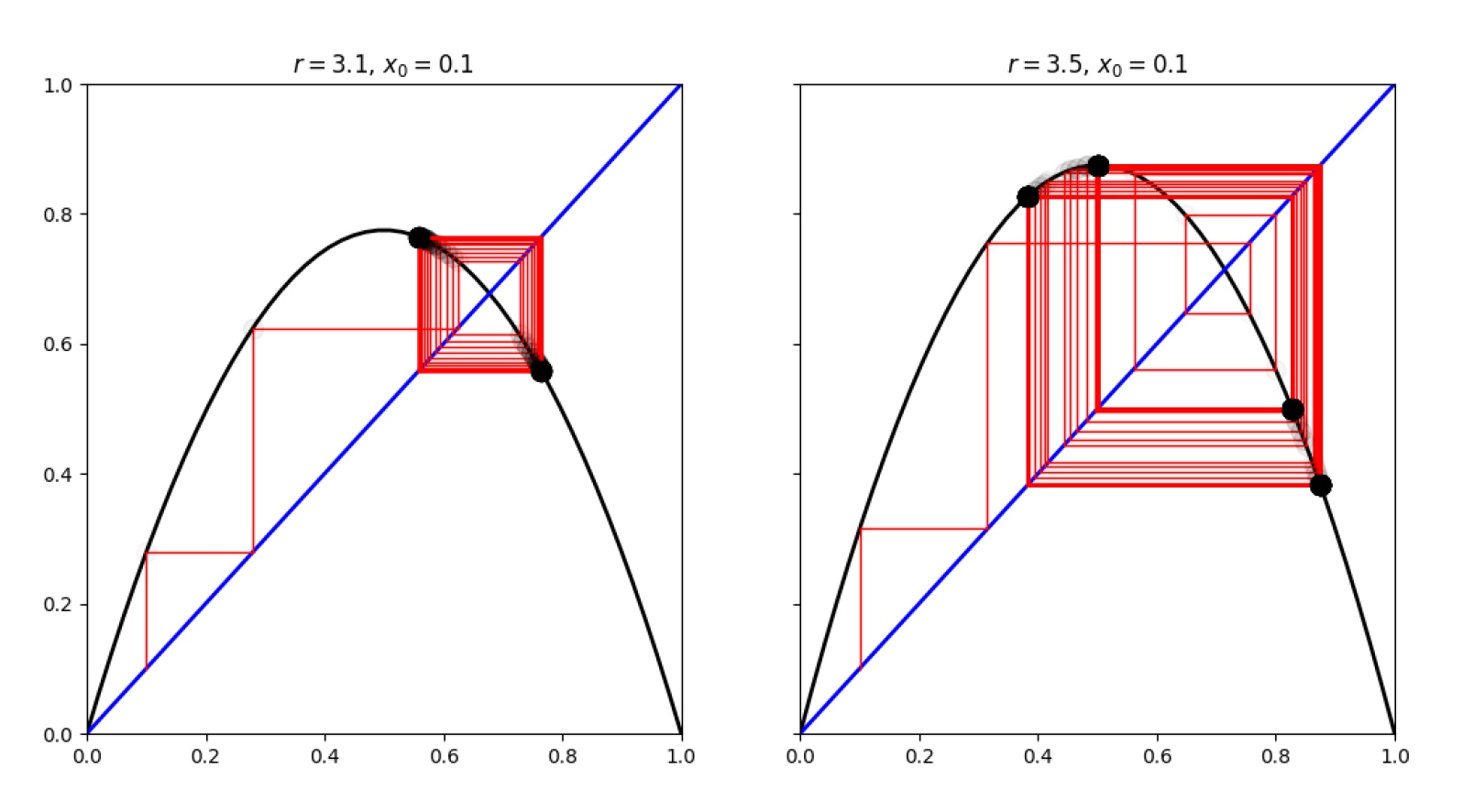
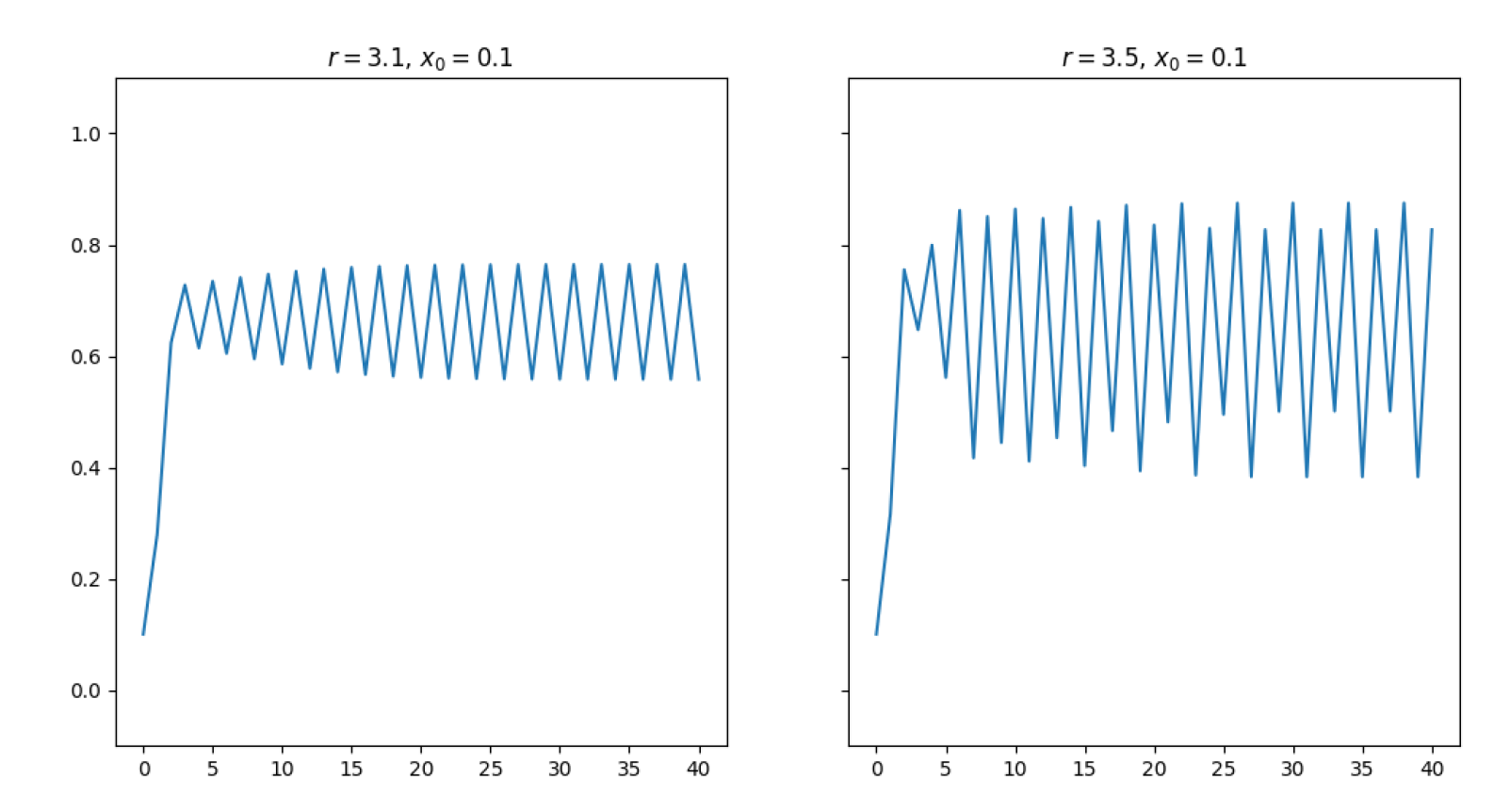
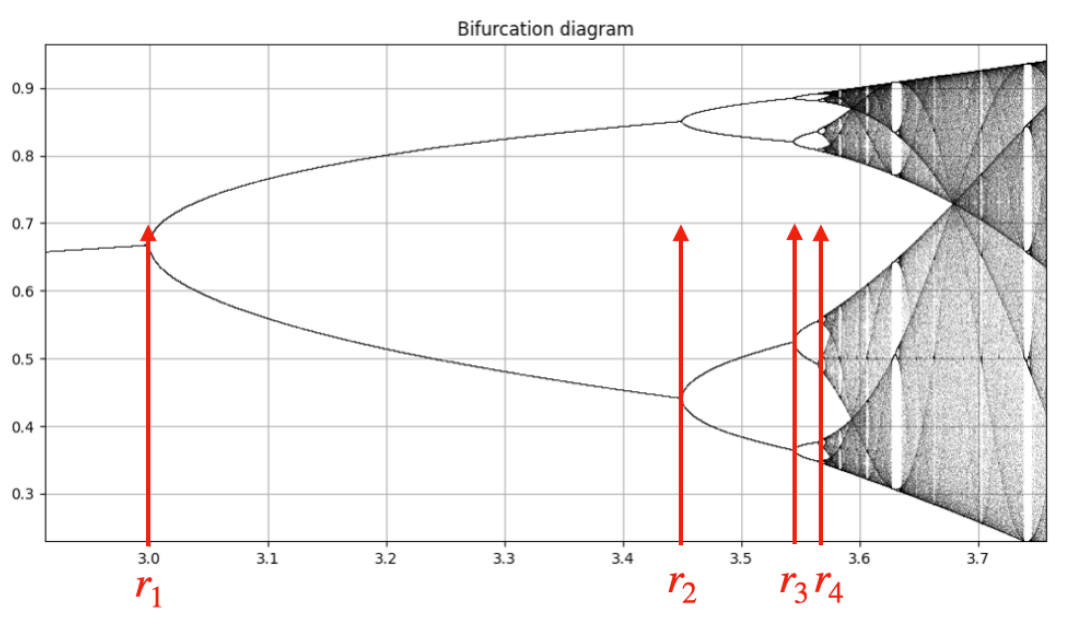
3.0<r⩽r3≈3.5:
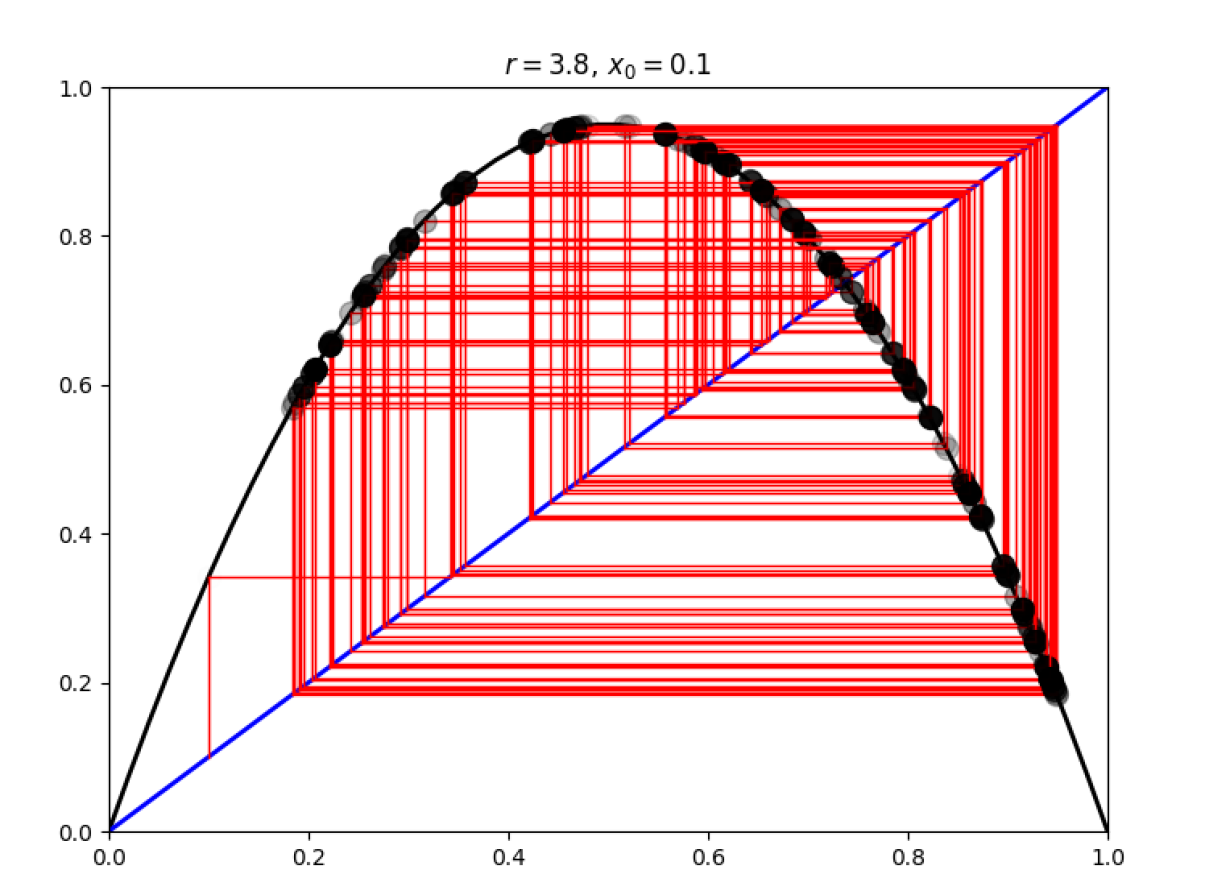
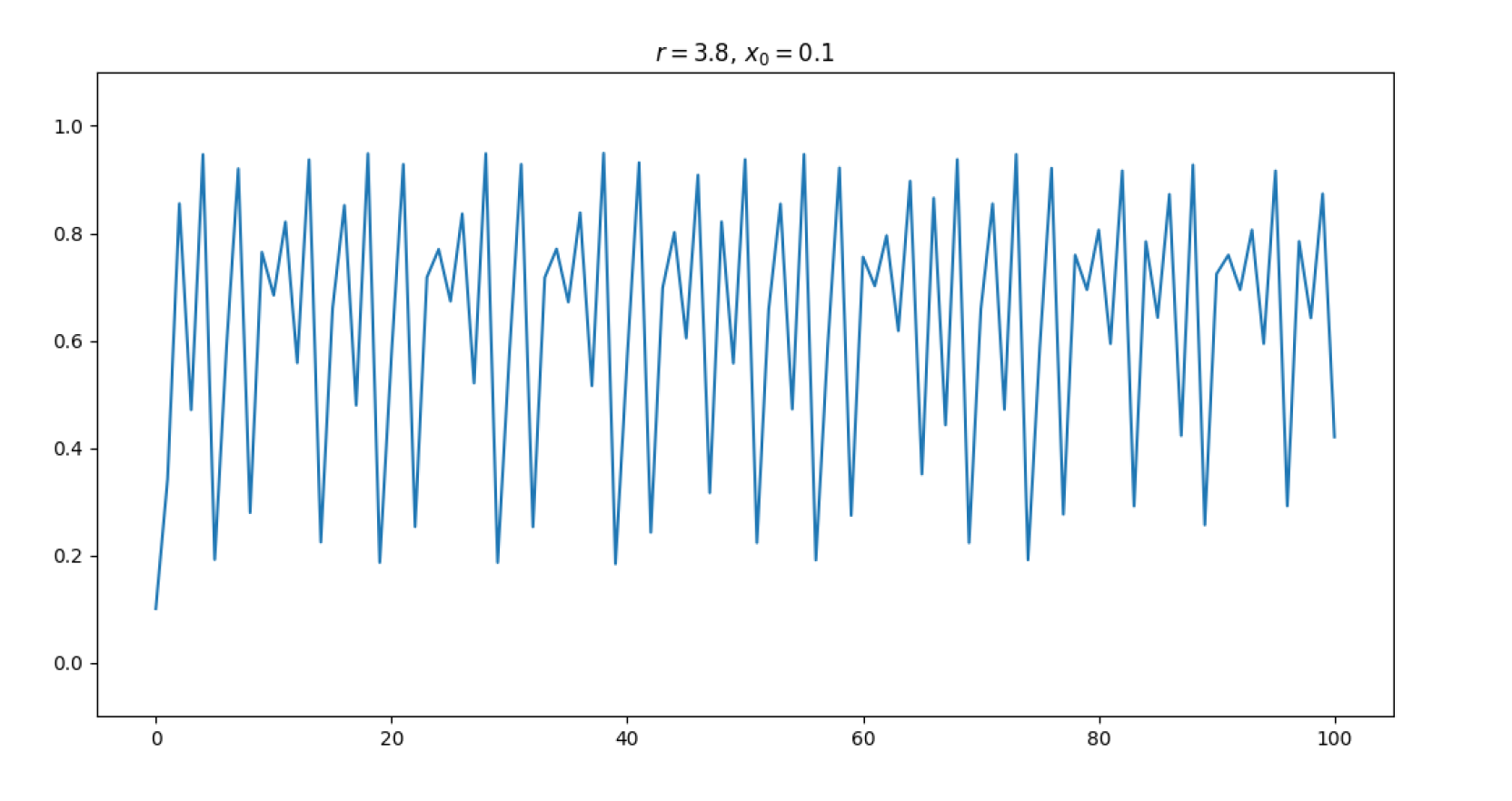
r>r3≈3.5:
不定点数量、取值与r大小之间的关系——分叉图:
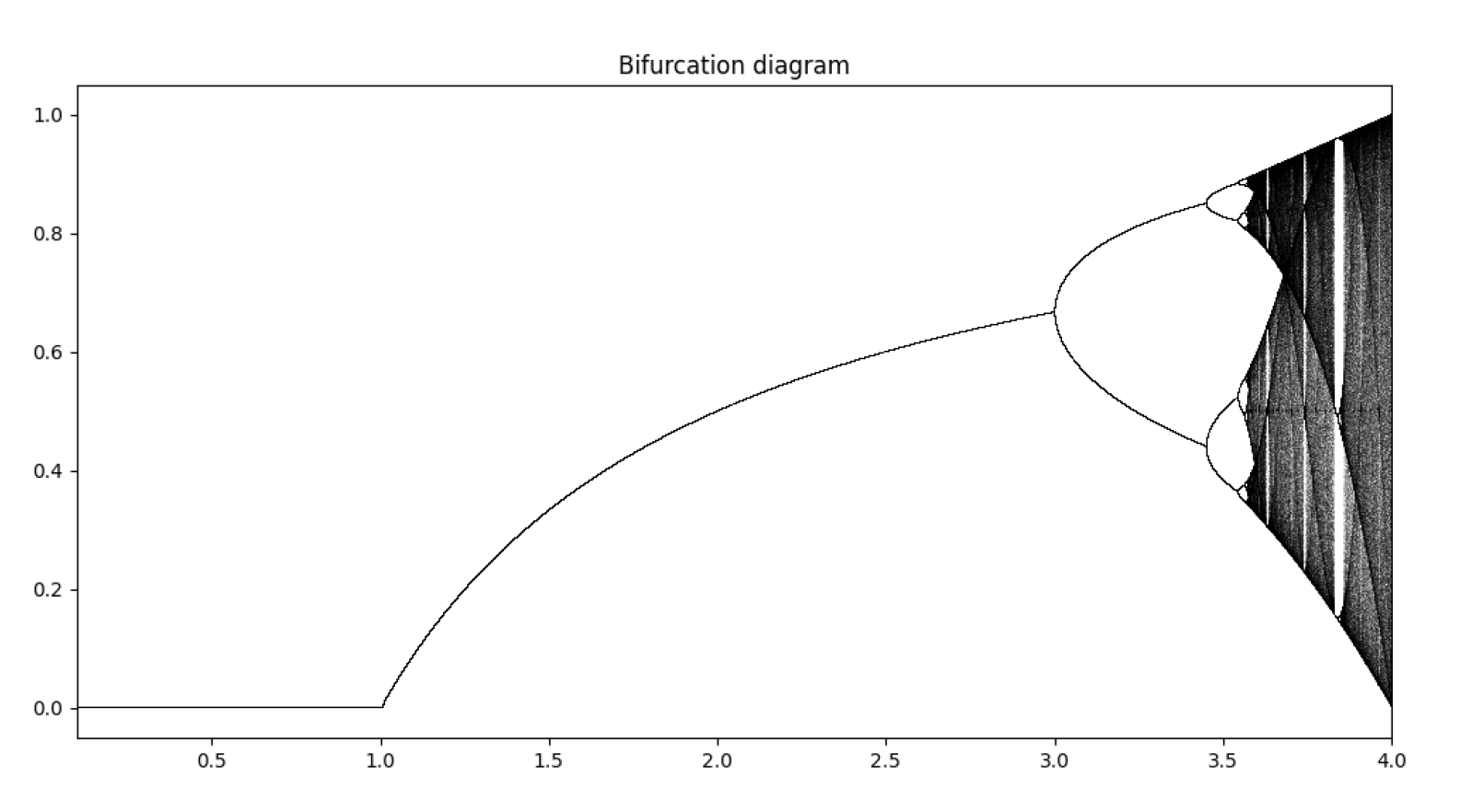
先对分叉图进行定性讨论:
- r<1:趋于灭绝,即经过足够多的迭代之后,xn→0。
- 1<r⩽3:趋于定态,即经过足够数量的迭代之后,xn固定在一个确定的值上定值则由r确定。
- 3<r≈3.5:周期变化,开始分叉时以2为周期,后又以4为周期。
- r>r3≈3.5:混沌态,轨迹点永不重复,不进入任何周期状态。
- r∈(r4≈3.83,r5≈3.86):系统会从混沌状态回到短暂的周期性,并且紧接着又回到混沌状态。此时的周期数为3的倍数。
(至于为什么r3,r4,r5等于上面的三个数值,后面有数学证明。)
理解分叉:
- 前两种状态比较好理解:分别对应蛛网图和折线图的前两张。
- 周期分叉的出现(当 (r>3.0) 时):由于周期性的存在,设系统存在的两个周期点分别为p 和 q,满足:
f(p)=q,f(q)=p
那么系统演化到这两点时将进入周期模式。
同时我们可以通过方程f(f(x))=x 求解这两个周期点:r[x(1−x)][1−rx(1−x)]=x
这是一个四次多项式方程,除去不动点 x1∗ 和 x2∗ 后,剩余两个解为:p,q=2rr+1±(r−3)(r+1)
∴ 当 r>3 时,系统开始出现2周期解,即分叉现象。
考察 f(f(x)) 在 p 和 q 处的导数:λ=dxdf(f(x))=r(1−2q)⋅r(1−2p)=r2[1−2(p+q)+4pq]
化简后得到:λ=−r2+2r+4
∴ 当 ∣λ∣<1.0 时,2周期解是稳定的,对应的参数范围为:3.0<r<1+6≈3.4494897
李雅普诺夫 (Lyapunov) 指数
当存在更多周期性,以至于趋于无穷多周期性时,我们应当如何定量刻画“混沌”?——李雅普诺夫指数。
定义:
从给定的x0初值,以及它附近的一个扰动δ0,经过多次迭代之后,在xn处存在一个偏离δn,那么我们可以用关系式
∣δn∣=∣δ0∣enλ
衡量。其中λ即为李雅普诺夫 (Lyapunov) 指数。容易发现,当λ为正数时,初值的敏感性极强,会发生混沌。
Calculation:
从 λ 的定义出发,我们有:
λ=n1ln∣∣∣∣∣δ0δn∣∣∣∣∣=n1ln∣∣∣∣∣δ0fn(x0+δ0)−fn(x0)∣∣∣∣∣
可以表示为导数的形式:
λ=n1ln∣(fn)′(x0)∣
将李雅普诺夫指数进一步展开,可以得到:
λ=n1lni=0∏n−1∣f′(xi)∣=n1i=0∑n−1ln∣f′(xi)∣
其中,xi 是每次迭代的结果。通过累加每次迭代的 ln∣f′(xi)∣,可以计算出李雅普诺夫指数。
- λ<0.0:系统处于定态或周期态。
- λ>0.0:系统趋于混沌状态。
定量普适性: 在分叉图中,除了得到表征混沌出现的李雅普诺夫指数外,我们同样可以发现,开始发生分叉的r值点之间的相对间距有固定比例,我们可以通过计算Feigenbaum常数δ来定量化描述这一特征:
δ=rn+1−rnrn−rn−1≈4.6692016...
易知和π、e一样,Feigenbaum常数也是一个普适的常数。
再看初值敏感性:
我们现在回过头来看初值敏感性:初值敏感性的存在是混沌中最重要的特征,由于无法精确地确定处置,比如由于实验测量误差或者计算中舍入和截断误差的存在,是的近似相同的初始值,在经过足够多的迭代之后,给出了完全不相同、看似随机的结果。因此又被通俗地称作“蝴蝶效应”——德克萨斯的蝴蝶扇动翅膀可能会引发一场龙卷。
线性微分方程
离散的差分→连续的微分
e.g. Logistic Equation的微分形式:
X˙=rN(1−KN)
对比离散形式:xn+1=rxn(1−xn),∴ 不动点意味着x∗=rx∗(1−x∗),即如果xn=x∗,则xn+1=xn。
∴xn+1−xn=0
微分形式又可写成:
ΔX=rN(1−KN)Δt
∴X˙=0⇒ΔtΔX=0⇒ΔX=0
可知与差分形式等价。(用到了海涅定理?这个不大确定sry……)
由上可以引出一维下不动点的定义:
如果x˙=f(x∗)=0,则x∗是该系统的不动点。
所以不动点即是非线性方程f(x)=0的零点,它可能有多个解(即存在多个不动点)。
不动点的稳定性
对于每个不动点:
- 可以从几何的角度去理解稳定性:根据它左右区域的正负来判断。
- f(x)>0:向右流动
- f(x)<0:向左流动
如果左右合流:该点稳定;左右分离:该点不稳定。
- 可以通过偏离不动点之后的变化特征来判断稳定性:假设不动点x∗附近有一个扰动η(t),那么对应x(t)=x∗+η(t)的动力学方程为:
dtd(x∗+η(t))=f(x∗+η)
对右侧进行泰勒展开:
f(x∗+η)=f(x∗)+f′(x∗)η+O(η2)⇒η˙=f′(x∗)η
- f′(x∗)>0:扰动随时间指数放大 ⇒ 不动点不稳定
- f′(x∗)<0:扰动随时间指数缩小 ⇒ 不动点稳定
- f′(x∗)=0:需要对更高阶η2进行分析
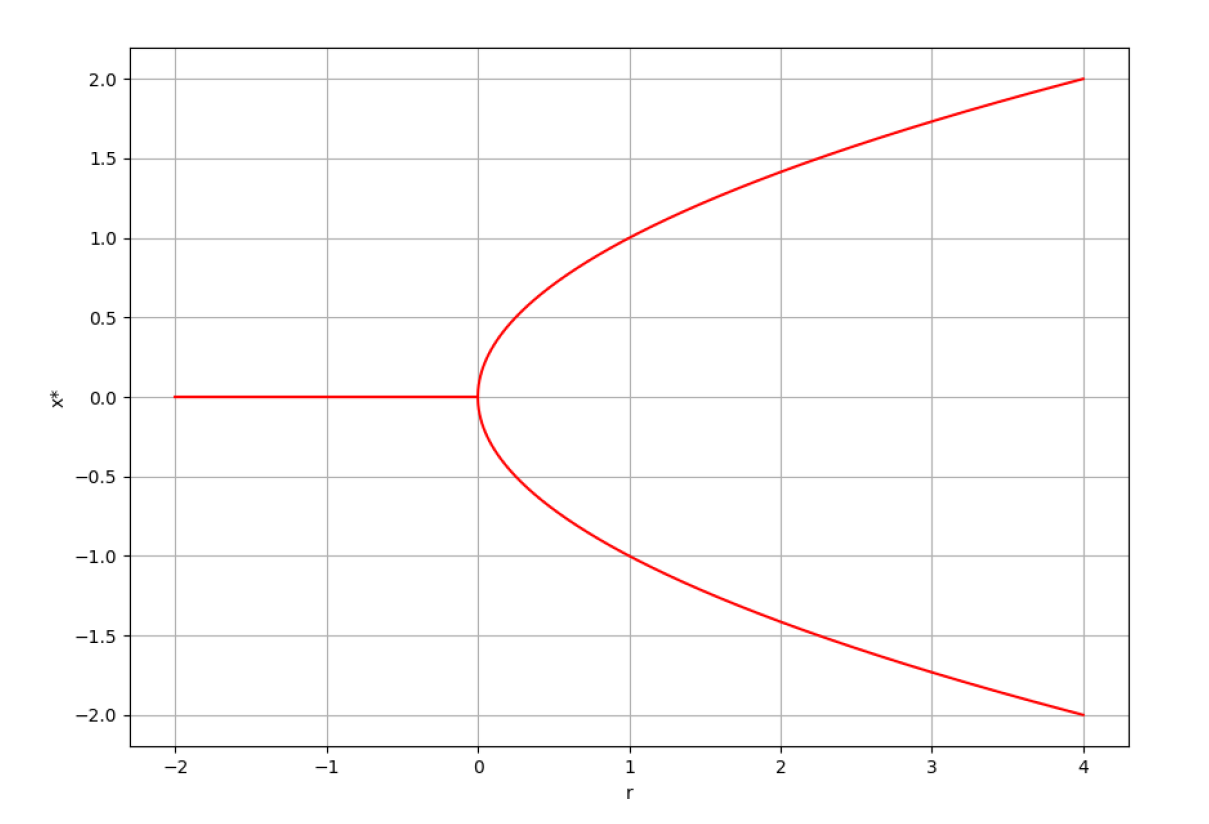
e.g. 对于动力学方程x˙=rx−x3,r取值不同,(实数域上)不动点数目及其稳定性不同:
- r⩽0:仅有一个不动点,该不动点是稳定的。
- r>0:它有三个不动点,r=0、r=±r。其中后两个是稳定不动点。
∴ 微分方程的参数发生变化时,系统不动点的状态也会发生变化。其中显著的现象就是分叉的出现。如下图所示。
多参数下的分叉和灾变
从上述例子可以看到,针对一个参数r时,当r取值不同方程不动点的稳定性也存在极大的不同,如果我们有多个参数,那么不动点的依赖情况又是什么情形?
例如,在上面的方程里多加一个常数项,x˙=h+rx−x3。对于不同的r和h值,其不动点的参数组合空间会更多。
灾变:当系统包含多个参数时,参数变化可能导致系统行为发生突然的、非连续的剧变,这种现象称为 “灾变”(Catastrophe)。
考虑上面非线性系统,当参数h=0.1时,其不动点分布如下图所示:
- 红色点:稳定不动点(吸引子)
- 黑色点:不稳定不动点(鞍点或排斥子)
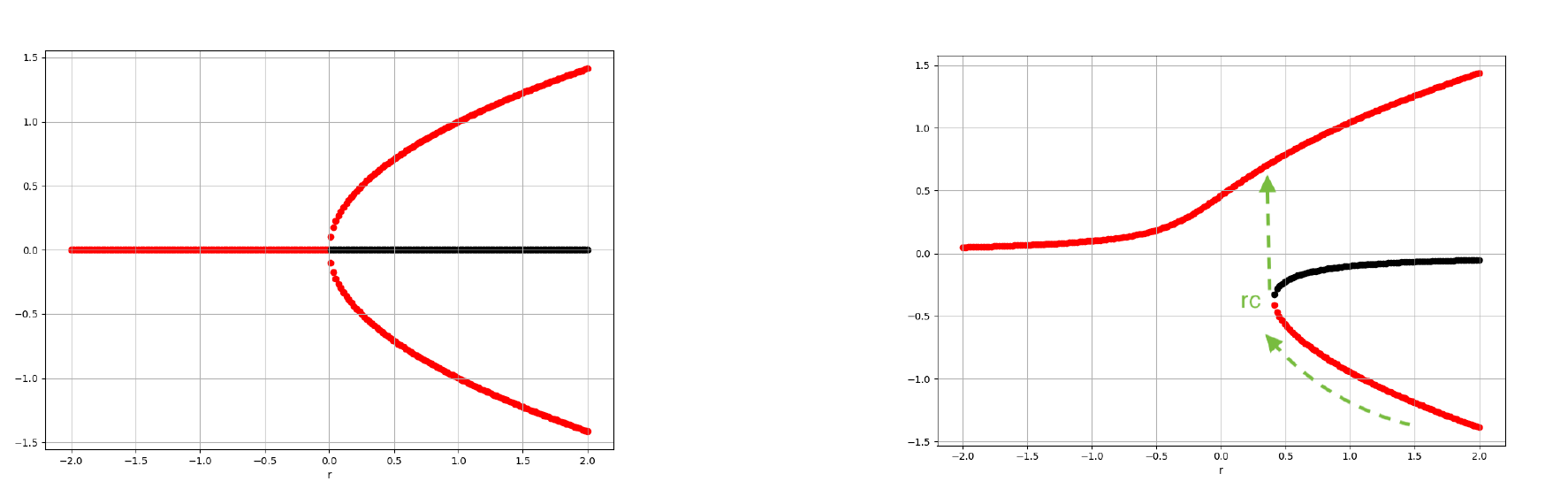
假设系统初始位于右下段的稳定态(红色点),当控制参数r变化到rc时,系统行为会发生突变:
- 临界点处:原有稳定不动点与不稳定不动点碰撞(鞍结分岔)
- 灾变发生:系统状态不连续跳跃至左上段的另一稳定态
二维非线性系统
二维动力学方程:
{x˙1=f1(x1,x2)x˙2=f2(x1,x2)
此时(x1,x2)就在相空间组成了一条随时间变化的轨迹曲线,而这种轨迹有多种可能性:
- 系统区域一个不动点x∗,但稳定性未知
- 轨迹组成一个周期性闭合轨道,x(t+T)=x(t)
- 在上面二者之间变化,无法预知
存在唯一性定理:
设一阶微分方程组:
dtdx=f(x,t),x(t0)=x0
其中 x∈Rn,f=(f1,...,fn)T 满足:
- 连续性条件:fi(x,t) 在域 D⊂Rn×R 上连续
- 利普希茨条件(Lipticz):存在常数 L>0,使得 ∀(x,t),(y,t)∈D:
∥f(x,t)−f(y,t)∥≤L∥x−y∥
那么将有下面结论:
- 解的存在唯一性:在某个区间 ∣t−t0∣≤h 上存在唯一解 x(t)
- 轨道不相交性:若 x1(t0)=x2(t0),则 ∀t 有 x1(t)=x2(t)
考虑非线性动力系统:
{x˙=f(x,y)y˙=g(x,y)
假设x∗, y∗是它的不动点,即满足:
f(x∗,y∗)=0; g(x∗,y∗)=0
在不动点附近加一个u(t),v(t)扰动,此时关于扰动的方程可以写成:
⎩⎪⎪⎪⎨⎪⎪⎪⎧u˙v˙=∂x∂fu+∂y∂fv=∂x∂gu+∂y∂gv
那么我们只需要关注它的Jacobbi矩阵的特征值。(很ODE的感觉……)
它的Jacobbi矩阵
A=(∂x∂f∂x∂g∂y∂f∂y∂g)
易知它有两个特征值λ1、λ2。
⇒
| 类型 |
特征值条件 |
相空间行为 |
| 排斥子 |
Re(λ1),Re(λ2)>0 |
所有轨道远离平衡点 |
| 吸引子 |
Re(λ1),Re(λ2)<0 |
所有轨道趋向平衡点 |
| 鞍点 |
Re(λ1)⋅Re(λ2)<0 |
有进有出(稳定与不稳定流形) |
| 中心 |
λ1,λ2=±iω (纯虚数) |
轨道形成闭合环 |
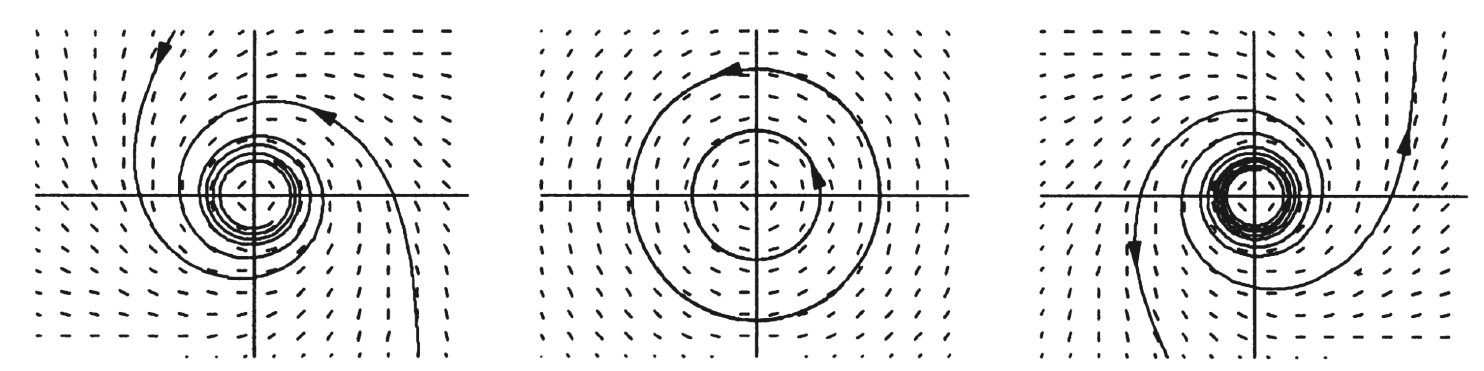
图示:
和ODE之间的区别:
(思考措辞ing)
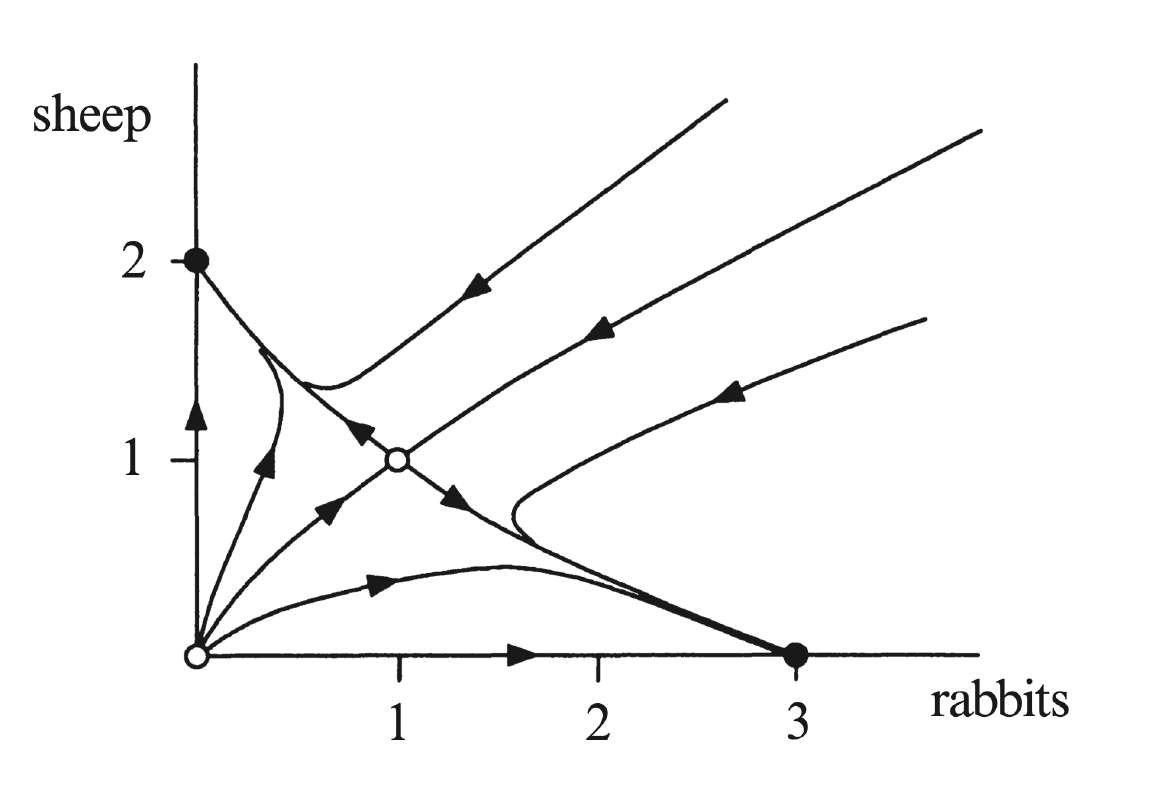
Lotka-Volterra模型:
经典的二维非线性系统。非线性项:xy。设简化后的方程如下:
{x˙=x(3−x−2y)y˙=y(2−x−y)
给定非线性系统,求得四个不动点坐标为:
(x∗,y∗)=(0,0),(3,0),(0,2),(1,1)
系统的雅可比矩阵为:
A=(3−2x−2y−y−2x2−x−2y)
分析不动点稳定性:
- 不动点 (0,0)
A(0,0)=(3002)
解得特征值:λ1=3, λ2=2,两个特征值实部均为正
∴ 稳定性:排斥子 (不稳定结点)
- 不动点 (3, 0)
A(3,0)=(3−60−62−3)=(−30−6−1)
特征值:λ1=−3, λ2=−1,两个特征值实部均为负
∴ 吸引子 (稳定结点)
- 不动点 (0, 2)
A(0,2)=(3−4−202−4)=(−1−20−2)
特征值:λ1=−1, λ2=−2,两个特征值实部均为负
∴ 吸引子 (稳定结点)
- 不动点 (1, 1)
A(1,1)=(3−2−2−1−22−1−2)=(−1−1−2−1)
特征值:
=λ=−1±2,特征值实部一正一负 ⇒ 鞍点
图示如下:
Lorentz方程
洛伦兹在1963年研究大气对流流动的动力学模型中得到的三维系统,其中非线性项主要来自xy和xz的耦合:
⎩⎪⎪⎨⎪⎪⎧x˙=σ(y−x)y˙=rx−y−xzz˙=xy−bz
性质:
(x,y,z)→(−x,−y,−z), f(x,y,z)=f(−x,−y,−z)
- 收缩性:
洛伦兹系统是严格耗散的,相空间体积随时间指数收缩:
V˙=∇⋅f=−σ−1−b<0
t→∞limV(t)=V(0)e(∇⋅f)t→0
所有轨迹最终收缩到零体积集合(吸引子)。
- 非周期性:由收缩性直接得出。反证法:假如存在周期性,那么最终系统将落入一个固定范围的相空间中,与它的收缩性是矛盾的。
分形













